分布式通信原语

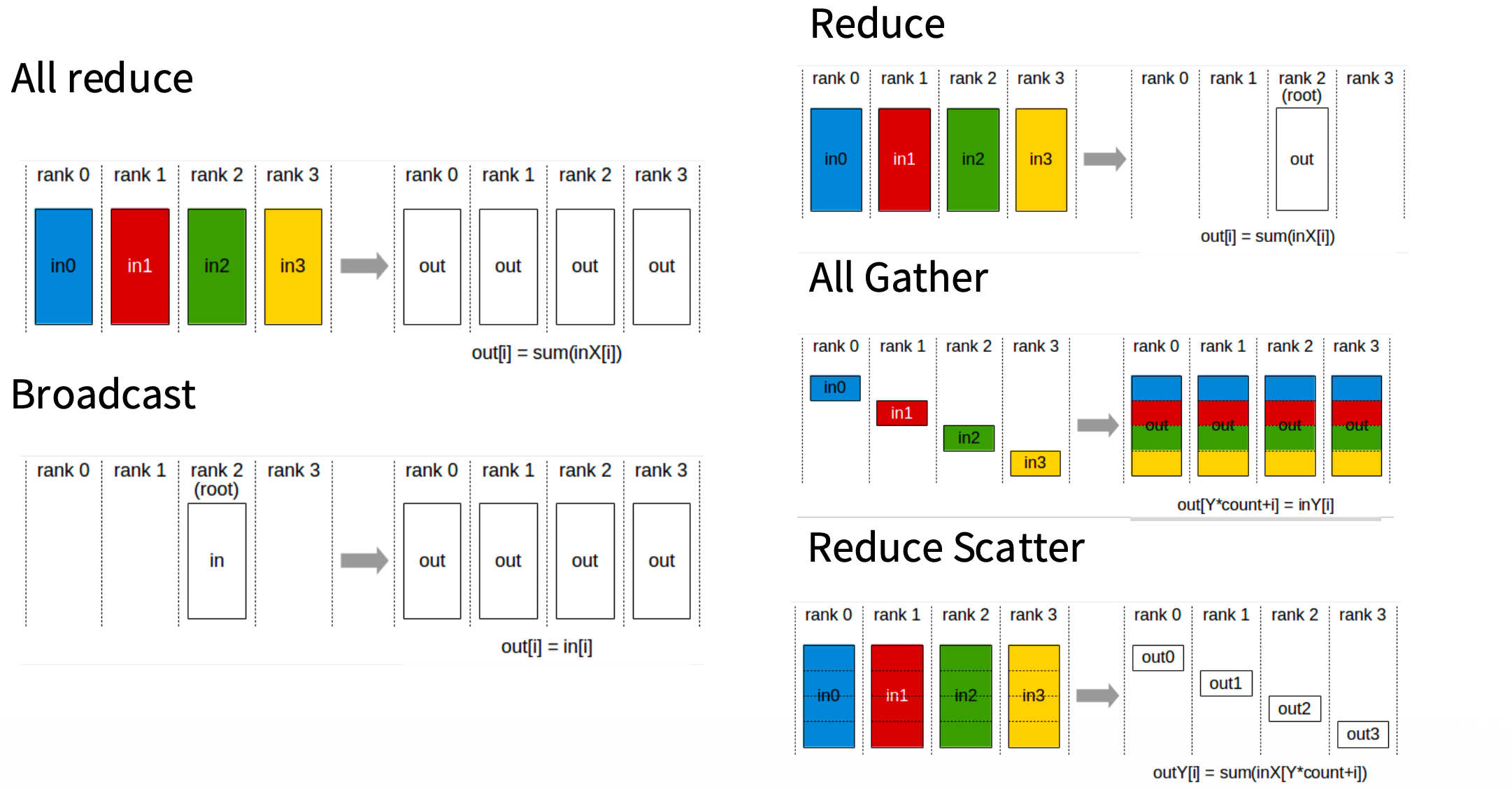
  • All reduce：根进程 $P_r$ 拥有一个大小为 $K$ 的消息缓冲区 $B$。操作结束后，通信组内的所有进程 $P_i$ 都拥有了 $B$ 的完全一致的副本。
  • Scatter：根进程 $P_r$ 拥有一个大向量 $V$，将其均匀切分为 $N$ 个块，记为 $v_0, v_1, \dots, v_{N-1}$。操作结束后，$P_i$ 仅获得对应的分块 $v_i$。
  • Gather：Scatter 的逆操作。每个进程 $P_i$ 拥有一个数据块 $v_i$。操作结束后，根进程 $P_r$ 将这些块按 Rank 顺序拼接，在其内存中形成完整向量 $V = [v_0, v_1, \dots, v_{N-1}]$。
  • All-Gather：每个进程 $P_i$ 拥有数据块 $v_i$。操作相当于先执行 Gather，再执行 Broadcast。操作结束后，每一个进程 $P_i$ 都拥有完整的向量 $V = [v_0, v_1, \dots, v_{N-1}]$。
  • Reduce：每个进程 $P_i$ 拥有一个向量 $X_i$。操作结束后，根进程 $P_r$ 获得结果 $R = X_0 \oplus X_1 \oplus \dots \oplus X_{N-1}$。
  • All-Reduce：逻辑上等价于 Reduce + Broadcast。操作结束后，所有进程 $P_i$ 都获得了完全相同的规约结果 $R = \sum_{j=0}^{N-1} X_j$。
  • Reduce-Scatter：逻辑上等价于先对全局数据做 Reduce 得到结果 $R$，然后将 $R$ Scatter 给各个进程。操作结束后，$P_i$ 获得结果向量的第 $i$ 个分块。
    常见集合通信原语示意图

LLM 训练中不同的并行策略

朴素数据并行 DP

数据并行中每个 GPU 都有一个完整的模型副本，输入 Batch 会被切分为多个 Mini Batch 并喂给不同的 GPU，每个 GPU 正常计算出梯度后，通过 All-Reduce 计算出全局梯度，再对参数进行更新。

  • 计算扩展性：每个 GPU 计算 B/M 个样本。
  • 通信开销： 2x#params，来自 All-Reduce 的过程。
  • 内存拓展性：无。每个 GPU 必须完整存储模型。

ZeRO

如下图所示，一个参数量为 $\Phi$ 的模型，进行 AMP 训练时，显存占用大致为：

  • 参数占 2$\Phi$ （2 指的是字节，BF16 为两字节）
  • 梯度占 2$\Phi$
  • 优化器状态 12$\Phi$ （FP32 参数、FP32 动量、FP32 方差）
    显存中参数构成

在朴素 DP 中， 每个 GPU 都要完全存储上面三个状态。微软 DeepSpeed 团队提出的 ZeRO 技术，逐步消除了上述三个部分的数据冗余。

  • Stage 1：切分优化器状态
    在 Stage 1 中，优化器状态被切分到不同的 GPU 上，每个 GPU 负责对一部分参数进行更新，然后通过 All Gather 让每个 GPU 都有一完整的更新后的参数。

具体来说，其算法步骤为：

  1. 每个 GPU 计算 Mini Batch 上的梯度；

  2. Reduce Scatter 梯度，这里产生了 #params 的通信开销；
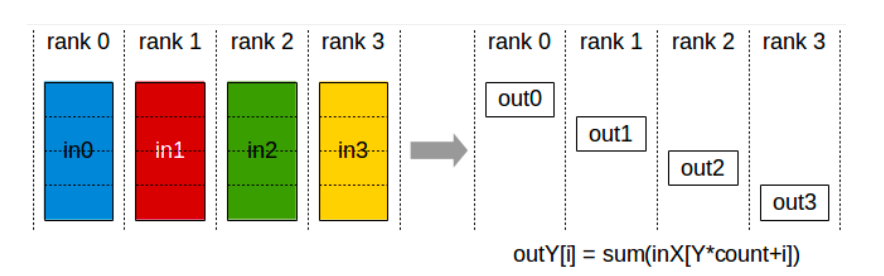
    Reduce Scatter 示意图

  3. 每个 GPU 根据它们自己维护的优化器状态对一部分参数做更新；

  4. All Gather 参数，这里产生了 #params 的通信开销。
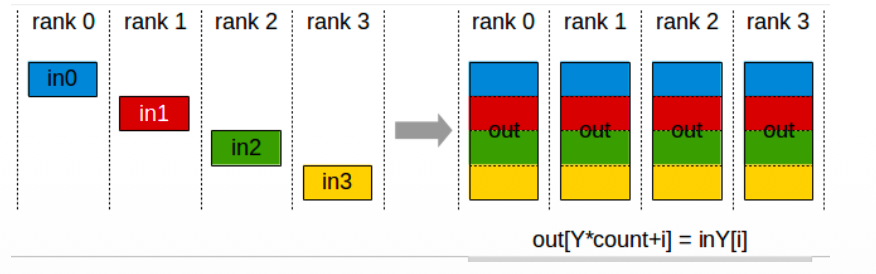
    All Gather 示意图

对比朴素 DP，Stage 1 就是将一个 All Reduce 操作替换为了 Reduce Scatter + All Gather，并将参数更新的步骤插入到二者之间。之前提过，All Reduce 与 Reduce Scatter + All Gather 是等价的，也就是说，我们在没有新增通信开销的情况下拿到了显著的内存收益。

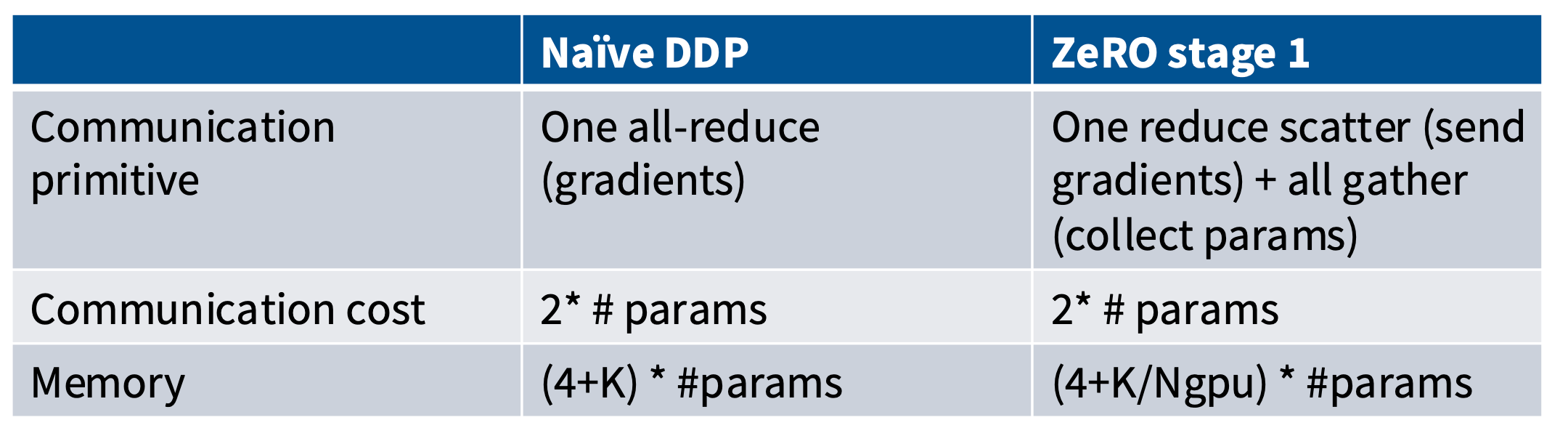
DDP v.s. ZeRO Stage 1

  • Stage 2：切分梯度和优化器状态
    在 Stage 2 中，我们尝试在 Stage 1 的来切分梯度。切分梯度，也就是每块 GPU 保留一小片空间用来存放自己负责的那个切片的梯度。在 Stage 1 中，我们需要先计算完所有的梯度后再对梯度做 Reduce Scatter。为了减少梯度的占用空间，必须得当梯度算完之后立刻做 Reduce Scatter，将其发送到存储这片梯度的 GPU 上，然后当计算图用不到时扔掉不属于自己的梯度。

具体来说，其算法步骤为：

  1. 计算一层梯度后，立刻做 Reduce Scatter 将其规约到正确的 GPU 上；
  2. 一旦梯度在计算图中再也用不到了，立刻释放对应的空间；
  3. 每个 GPU 更新参数；
  4. 对参数做 All Reduce。

相比 Stage 1，其通信开销保持不变。在 Stage 1 中对梯度做的一次性 Reduce Scatter 在 Stage 2 中被拆分为多次，但是彼此没有重合，所以整体通信开销不变。

  • Stage 3 (FSDP)：切分梯度 + 优化器状态 + 参数
    在 Stage 3 中，参数也被切分，因此进行前向计算时，需要通过通信获取完整参数。如下图所示，在进行前向和反向计算钱，使用 All Gather 获取完整的权重再进行下一步的计算。
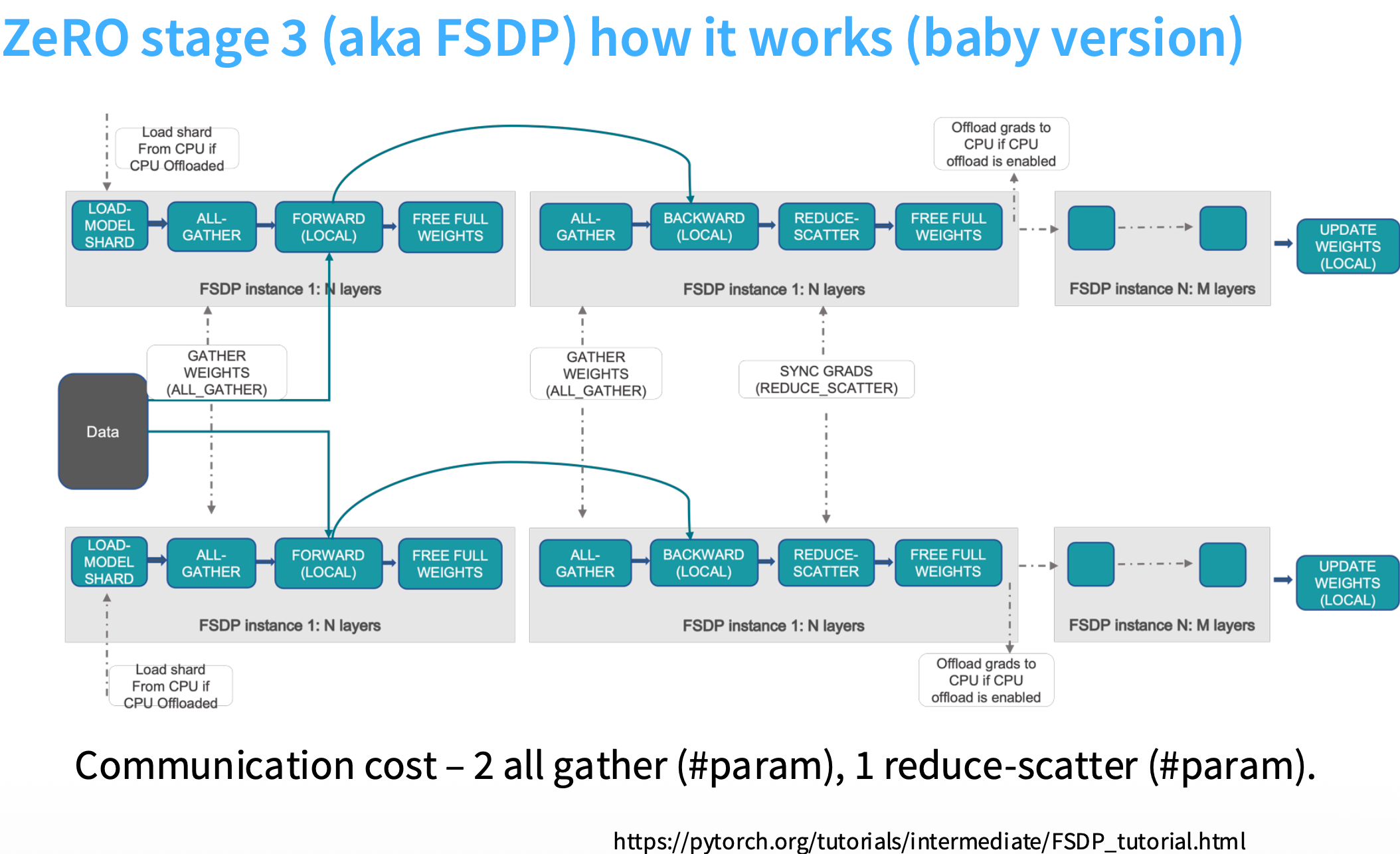
    Stage 3 简单示意图

每次计算前都要做一次 All Gather，这里面的通信开销非常大，但是也并非慢到无法接受。这得益于 Stage 3 将通信和计算折叠：如下图所示，除了第一个前向计算 FWD0 之外，其他的前向计算需要的通信都可以与前一此计算重叠，如果前一层的计算时间大于拉取下一层的时间，通信延迟还能够被完全隐藏。
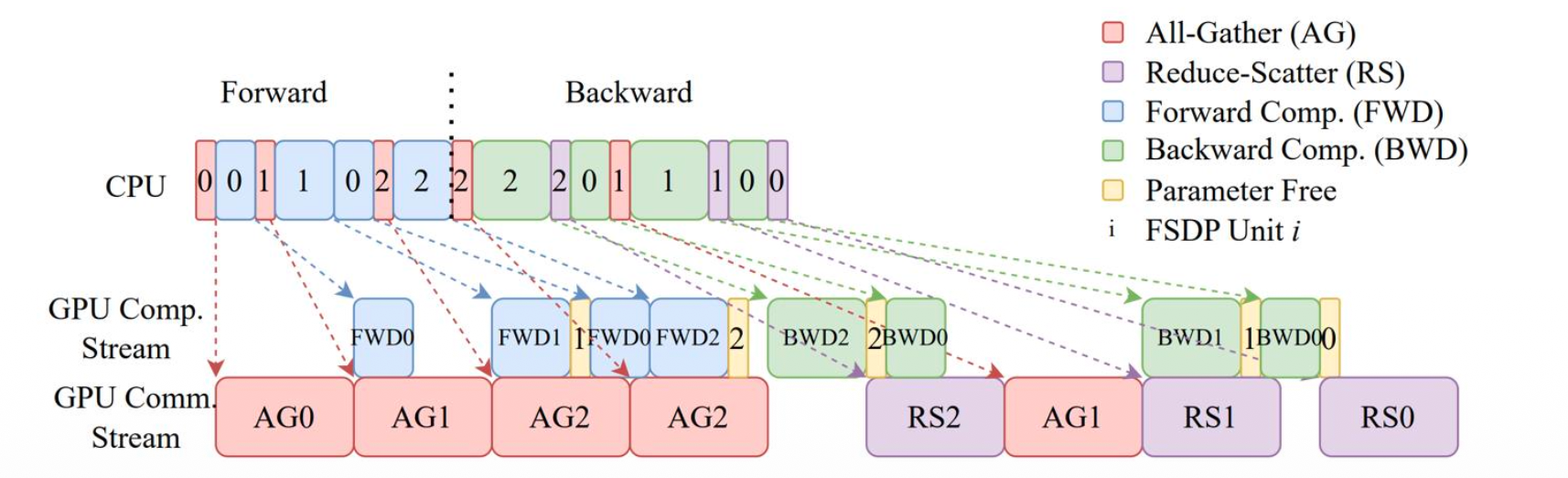
PixPin_2026-01-18_17-56-09.webp

Stage 3 的通信量是 3 x #params，包括前向和反向各一次的 All Gather 和计算梯度时的 Reduce Scatter，是 Stage 2 的 1.5 倍。

DP 的限制

Data Parallelism 不是万能，其有如下限制：

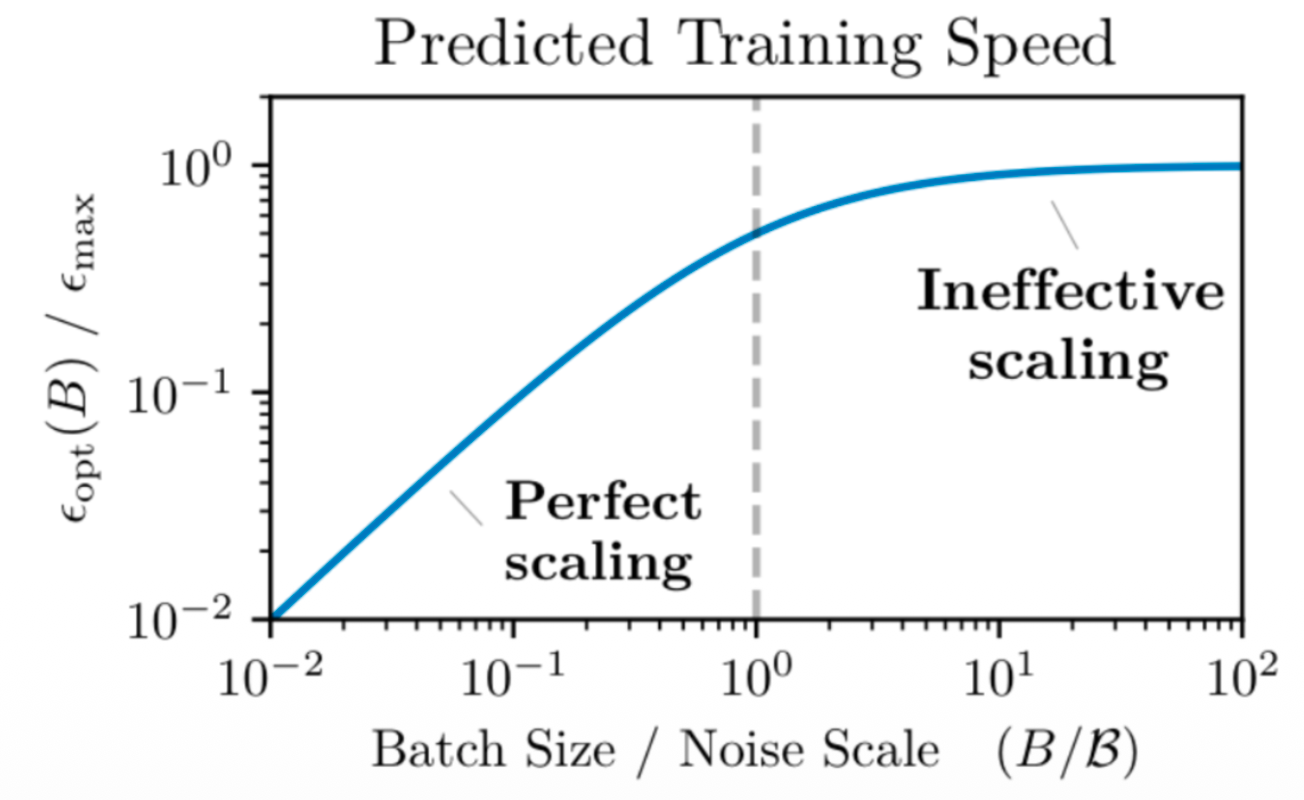
  1. DP 并行数必须小于 Batch Size。Batch Size 不是越大越好，当 Batch Size 过大时，其所需要的训练步数并不能同比下降，也就是模型并不能学的更快。而 DP 的并行数必须得小于 Batch Size，这就约束了 DP 并行的上限。
    训练速度与 Batch Size 的关系
  2. ZeRO 各有优劣。Stage 1 和 2 几乎没有额外开销，但是没有切分模型；Stage 3 有额外的开销并且不能减少激活值的内存。

模型并行 Data Parallelism

在 ZeRO Stage 3 中我们将对激活值做切分，从而解决数据并行中难以扩展内存的痛点。在模型并行中，也会将参数切分到不同的卡上，但是卡间交换的是激活值而非参数。模型并行有两类实现，包括流水线并行和张量并行。

流水线并行 Pipeline Parallelism

流水线并行指的是将不同的层切分到不同的卡上，数据像流水线一样在 GPU 之间流动。这是一个很符合直觉但是实现比较困难的并行策略。如下图所示，如果再等待其它卡的过程中什么也不干，每张卡只有 1/n 的时间处于激活状态，效率极其低下。
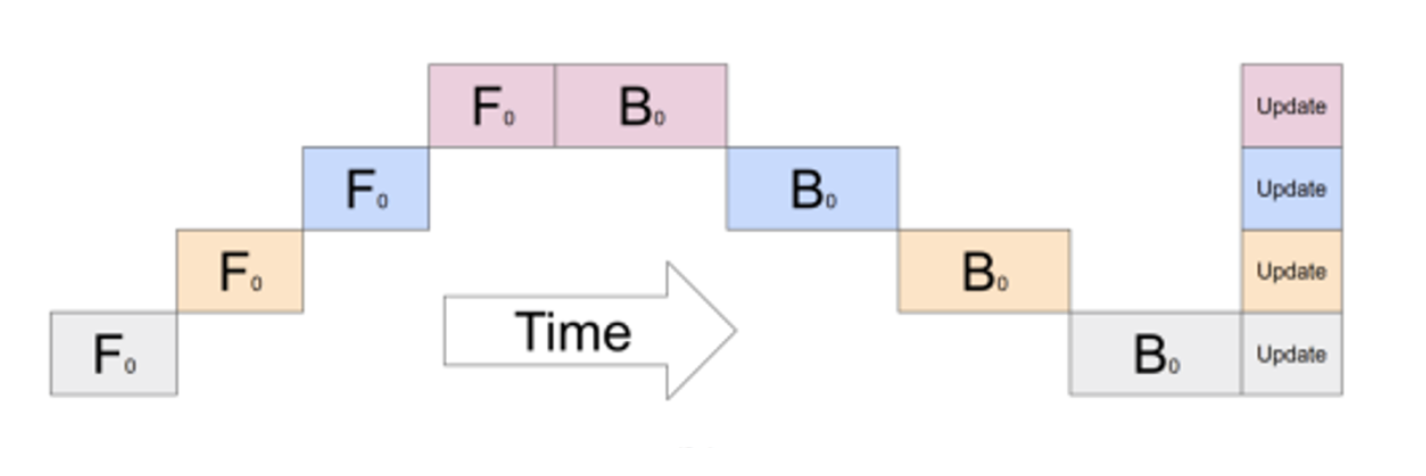
低效的流水线并行

对此的解决策略是将一个 Batch 分割多个小 Batch，并依次送入流水线中。如下图所示，将数据分割为四条送入流水线，仍会有一些空泡，但是整体效率相比上面的朴素实现得到了提升。整体的空泡率为：$(n_\text{stages}-1)/n_\text{micro}$，Micro Batch 越多，空泡率越少。但是，与模型并行一样，Micro Batch 同样受限于 Batch Size。
流水线并行示意图

既然 PP 也没多好，为啥使用它？

  1. 相比 DP，PP 能够节省显存，它不仅对参数进行了切分，还对激活值进行了切分。
  2. PP 只需要进行点对点的通信，很适合部署在通信链路效率不高的机器之间。

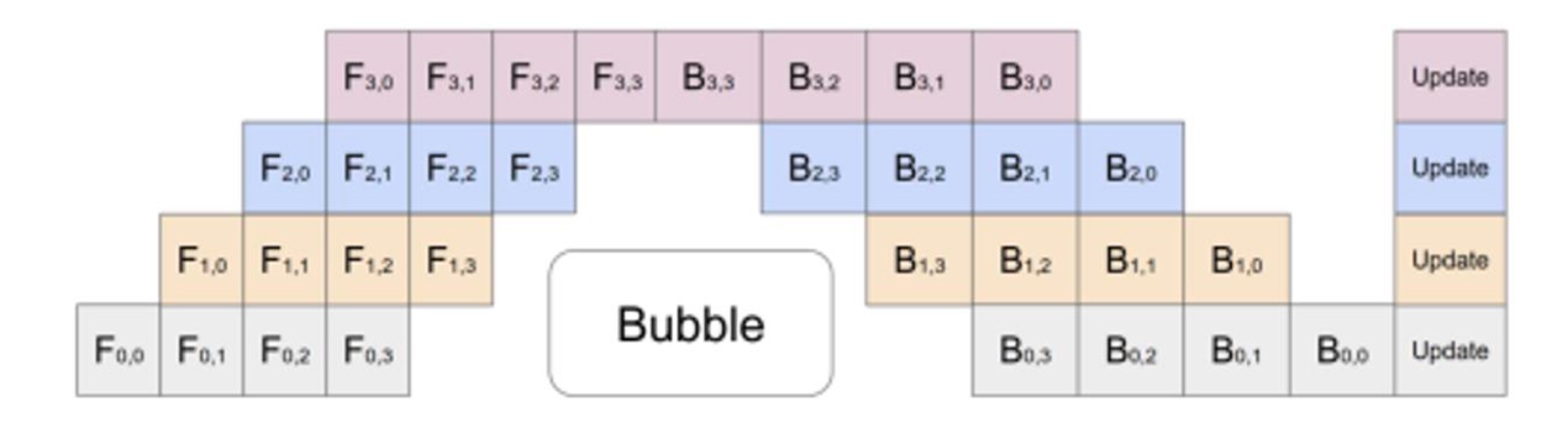
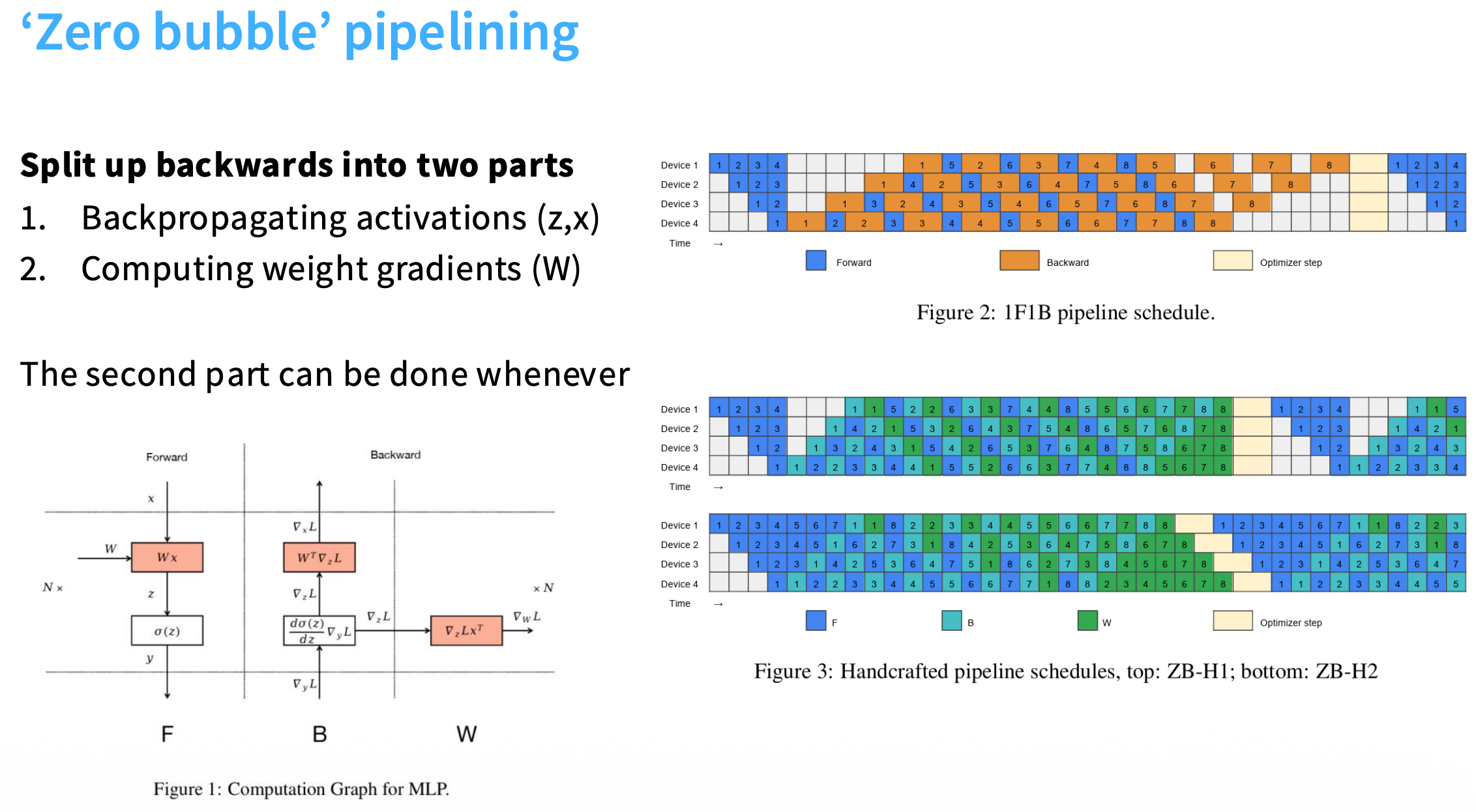
最后还介绍了 Zero Bubble Pipeline。具体来说，反向计算可以分成两步，第一步是计算对输入的微分 B，第二步是计算对权重的微分 W。其中，对输入的微分是前一层依赖的 OutGrad，必须尽可能快地计算；后者是不被其它卡依赖的，只要在梯度更新前算完即可。Zero Bubble Pipeline 的核心思想就是优先完成 B，当流水线空闲时再完成 W。当然，这只是一个 High level 的介绍，老师一直在强调在工程实现中不管是这个 Zero Bubble Pipeline 还是单纯 PP，其实现起来都相当困难。

PixPin_2026-01-18_18-53-29.webp

张量并行 Tensor Parallelism

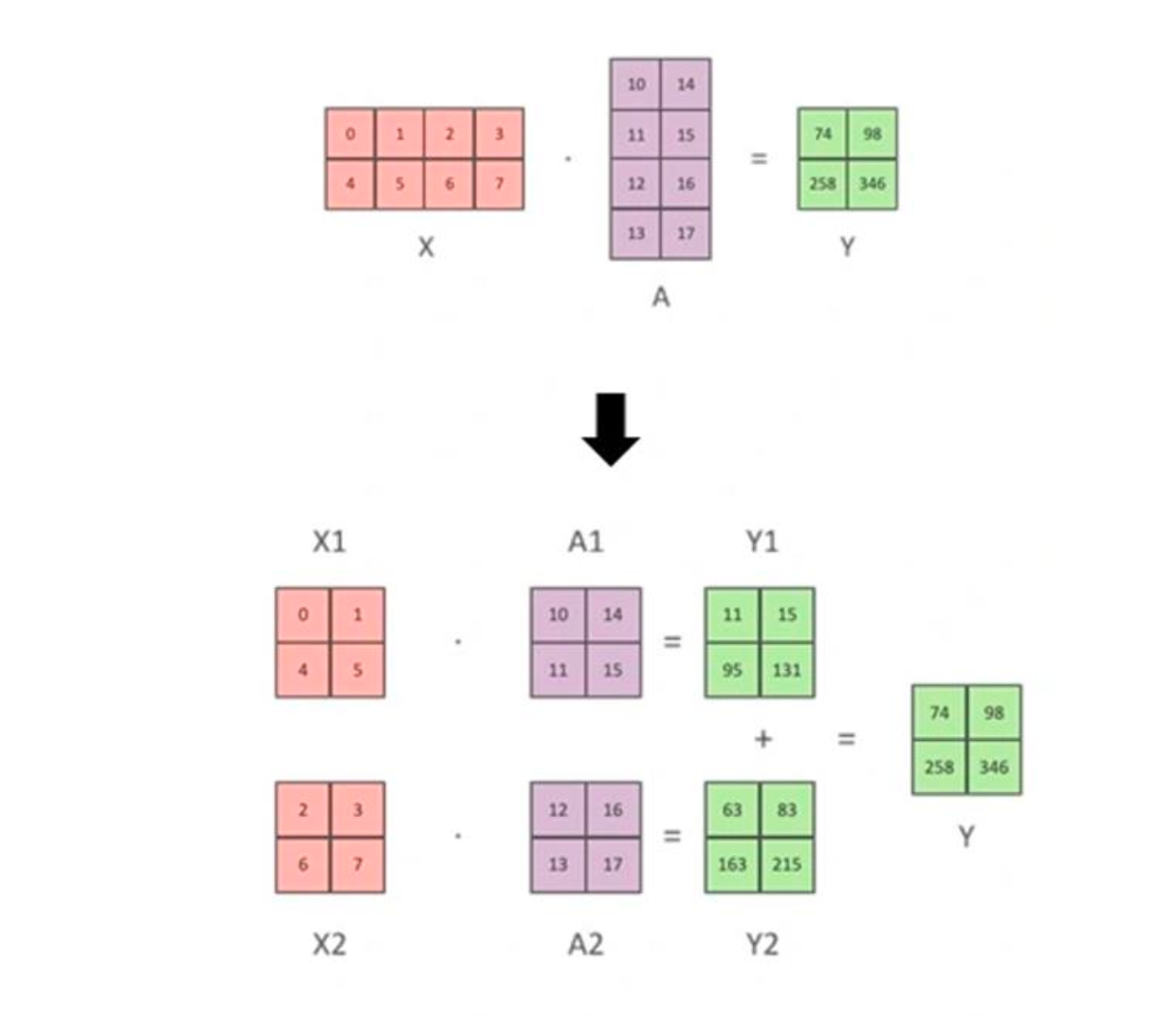
流水线并行可以认为是沿着纵轴对模型切分，张量并行则是对横轴切分，即将一个大的矩阵运算切分到两张卡上，如下图所示，X@A = X1@A1 + X2@A2 = Y。
矩乘切分
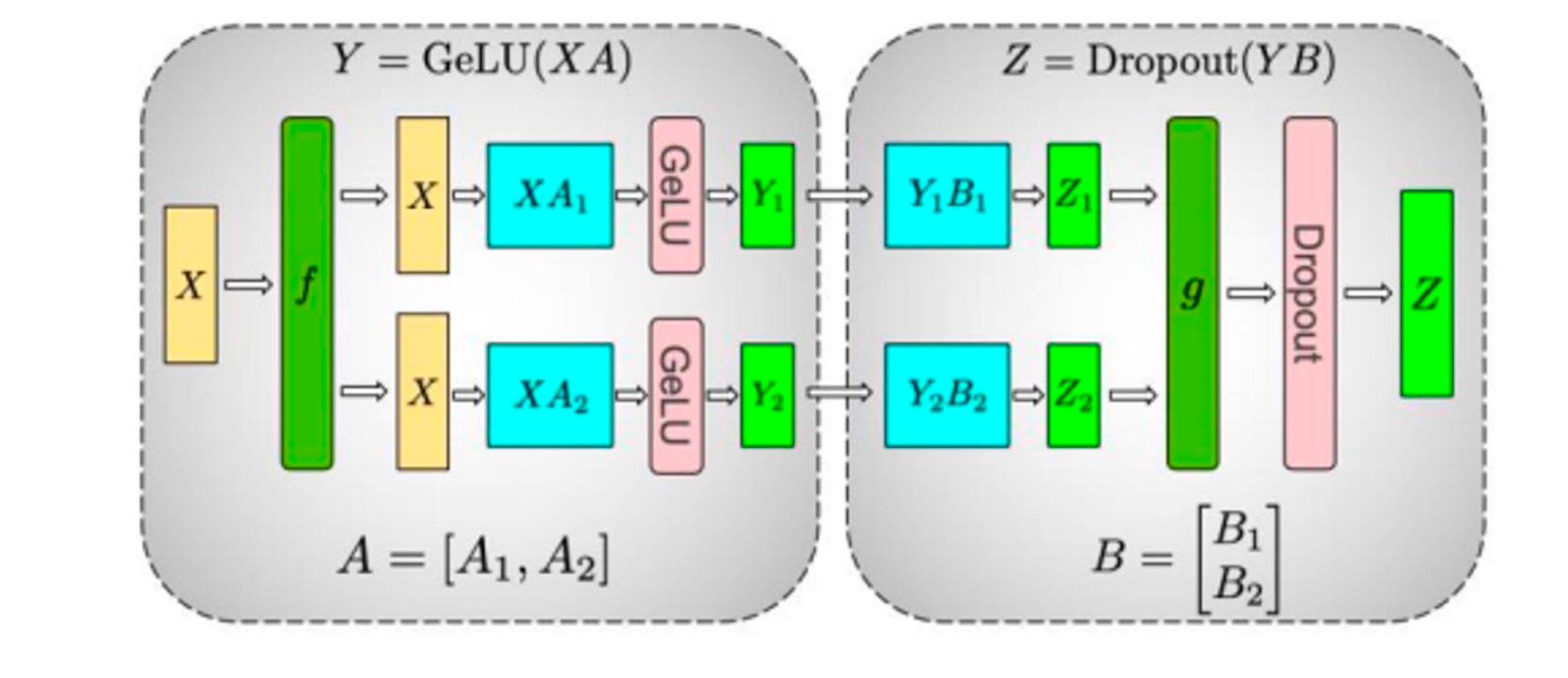
下图展示了一个 MLP 网络中的标准切分方式：第一个矩乘的权重按列切分，第二个按行切分。

前向的流程是：输入 X 通过恒等映射 f 复制到所有卡上，GPU 1 计算出 XA1，GPU 2 计算出 XA2，由于激活函数是逐元素独立计算的，因此无需与其它 GPU 通信。此时 GPU 1 正好持有按按列切分的 Y1，GPU 2 持有 Y2，这与行切分的 B 在维度上完美对应，不需要进行 All Gather 操作即可继续流转到第二个矩乘上。然后再经过 All Reduce 操作 g 对输出进行聚合，就可以得到完整的 Z。

反向的流程与前向类似，只是操作 g 变成了恒等映射，操作 f 变成了 All Reduce 操作。
MLP 网络中 TP 切分方式

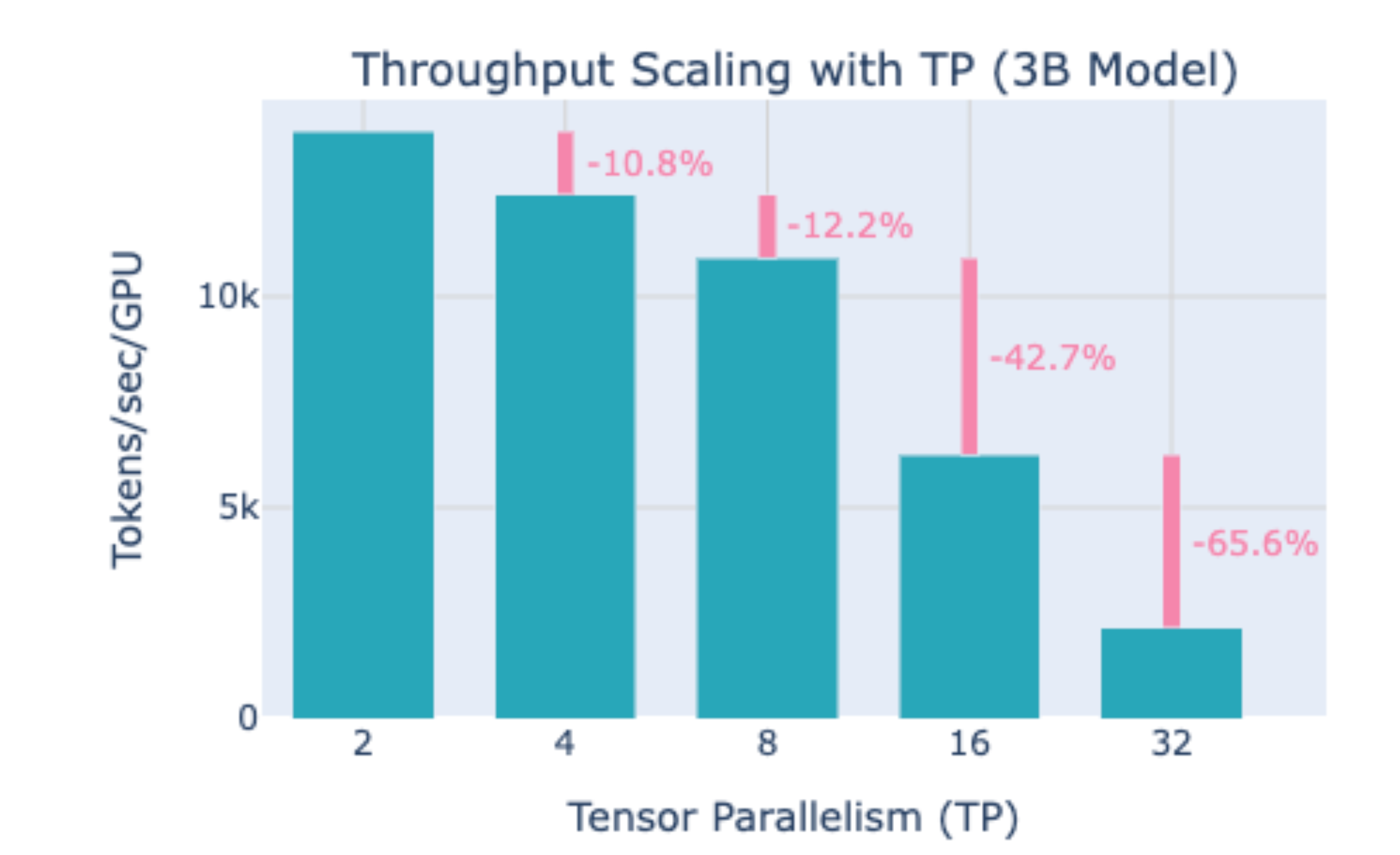
TP 在每一层中都需要进行大量的通信，因此其对通信要求很高。如下图所示，当 TP 并行度大于 8 时，单卡吞吐量显著下降。同一个节点内的卡通信速度很快，通常 TP 在一个节点内的 8 张卡上部署。

单卡吞吐量随 TP 数变化

序列并行 Sequence Parallelism

目前介绍的 TP 和 PP 都是对模型参数进行切分的，但是没有切分激活值。在训练过程中，模型的激活值可以通过以下公式来估算：

$$ \text{Activations memory per layer} = sbh \left(34 + 5 \frac{as}{h}\right) $$

其中变量含义如下：

  • $s$ (sequence length): 序列长度
  • $b$ (microbatch size): 微批次大小
  • $h$ (hidden dimension size): 隐藏层维度
  • $a$ (number of attention heads): 注意力头数

激活值由两部构成，第一部分是线性项，来自 MLP 、Attention 中的线性投影和 LayerNorm；第二部分是二次项 $5bas^2$，这部分来自 Attention 机制，包括注意力分数、Softmax 结果等，这部分可以通过 Flash Attention 的重计算消除。

应用 TP 后，显存占比中线性部分中的系数 24 可以减少为 $1/t$，其中 t 是 TP 并行度。，没有变化的系数 10 来自非 Matmul 的部分，包括 LayerNorm（4）、Dropout（2）、Attention 和 MLP 的输入（4）。

$$ \text{Activations memory per layer} = sbh \left(10+\frac{24}{t} + 5 \frac{as}{h}\right) $$

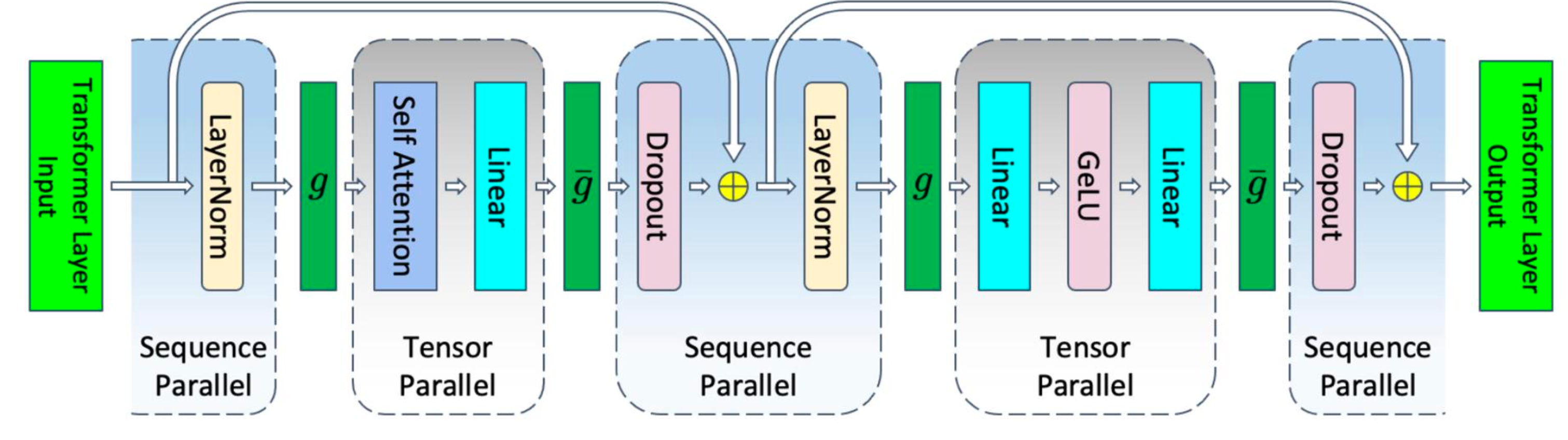
以 LayerNorm 为例，其对每一条序列独立地做 Norm，因此可以通过在序列维度上进行切分，从而降低显存占用。如下图所示，在 LayerNorm 和 Dropout 上做了序列并行，在前向中，LayerNorm 的输出需要经过一次 $g$ All Gather 以将完整 Tensor 送入 Attention，Dropout 的输入需要经过一次 $\bar{g}$ Reduce Scatter 以将完整 Tensor 按序列切分。在反向中，$g$ 和 $\bar{g}$ 操作交换。
序列并行示意图

应用 SP + FA 后，模型整体的激活值可以降低为 $sbh \left(\frac{34}{t}\right)$。

Configuration Activations Memory Per Transformer Layer
no parallelism $sbh \left(34 + 5\frac{as}{h}\right)$
tensor parallel (baseline) $sbh \left(10 + \frac{24}{t} + 5\frac{as}{ht}\right)$
tensor + sequence parallel $sbh \left(\frac{34}{t} + 5\frac{as}{ht}\right)$
tensor parallel + selective activation recomputation $sbh \left(10 + \frac{24}{t}\right)$
tensor parallel + sequence parallel + selective activation recomputation $sbh \left(\frac{34}{t}\right)$

Ring Attention 和 专家并行

最后简单介绍了下 Ring Attention 和专家并行。

Ring Attention 解决的痛点是超长序列中单卡装不下 KV Cache，其核心思想是将 KV 进行切分，GPUs 之间以环的形式流转 $KV_i$，并计算出相应的结果。

专家并行则是将专家散布到不同的 GPU 上，会面临来自负载均衡和计算通信 Overlap 的挑战。

使用并行策略扩大 LM 的规模并训练

3D 并行

3D 并行指的是混合使用 DP、PP 和 TP 策略，一个简单的原则是：

  • 先将模型切分到单卡放得下
    • 使用 TP 策略，TP 并行度不大于每个节点内 GPU 的数量
    • 在节点之间使用 PP 或者 ZeRO Stage 3，取决于带宽大小
  • 扩大 DP 规模直至达到 GPU 上限