TL;DR 本讲是 CS336 系列笔记的第五讲。本讲从 GPU 的设计理念出发,梳理了 SM/SP 计算架构与内存层级体系,并结合 Roofline 模型,重点解析了访存合并、算子融合、重计算及分块(Tiling)等核心优化策略。此外,还应用上述策略,粗略推导了 FlashAttention 如何利用 Online Softmax 技术打破显存带宽瓶颈,实现 IO 感知的极致加速。
GPU 架构
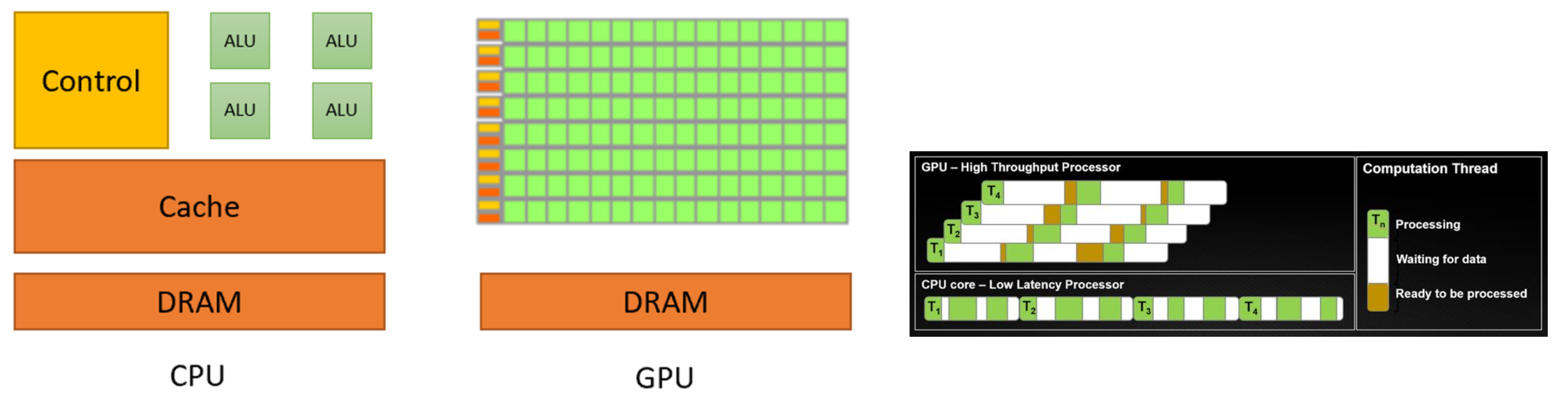
CPU 与 GPU 设计理念
从架构上看,CPU 有一个很大的控制单元,而 GPU 中计算单元占主导。这揭示了二者在设计理念上的区别:CPU 致力于降低执行延迟,GPU 致力于提高计算吞吐量。
GPU 计算单元架构
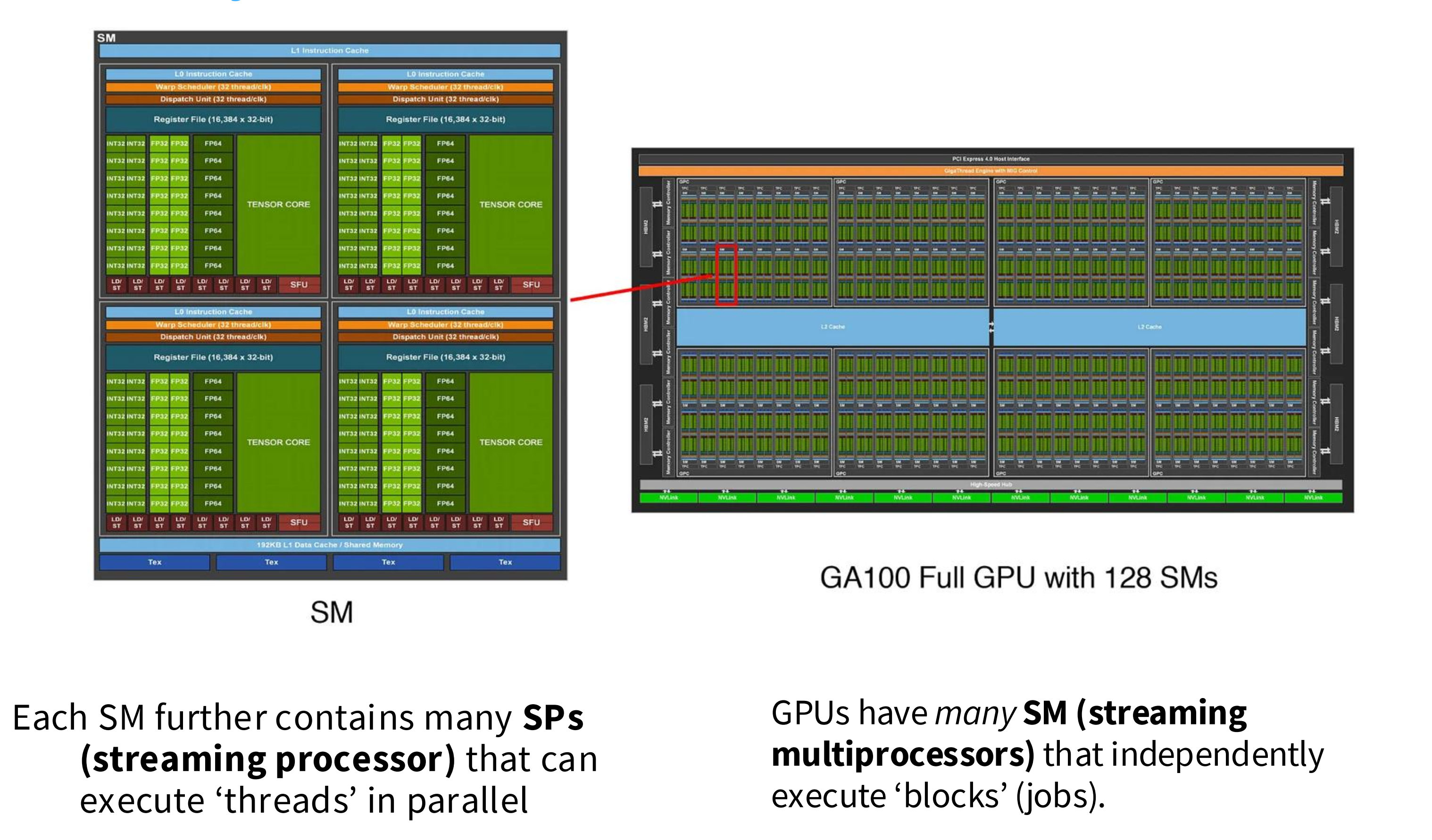
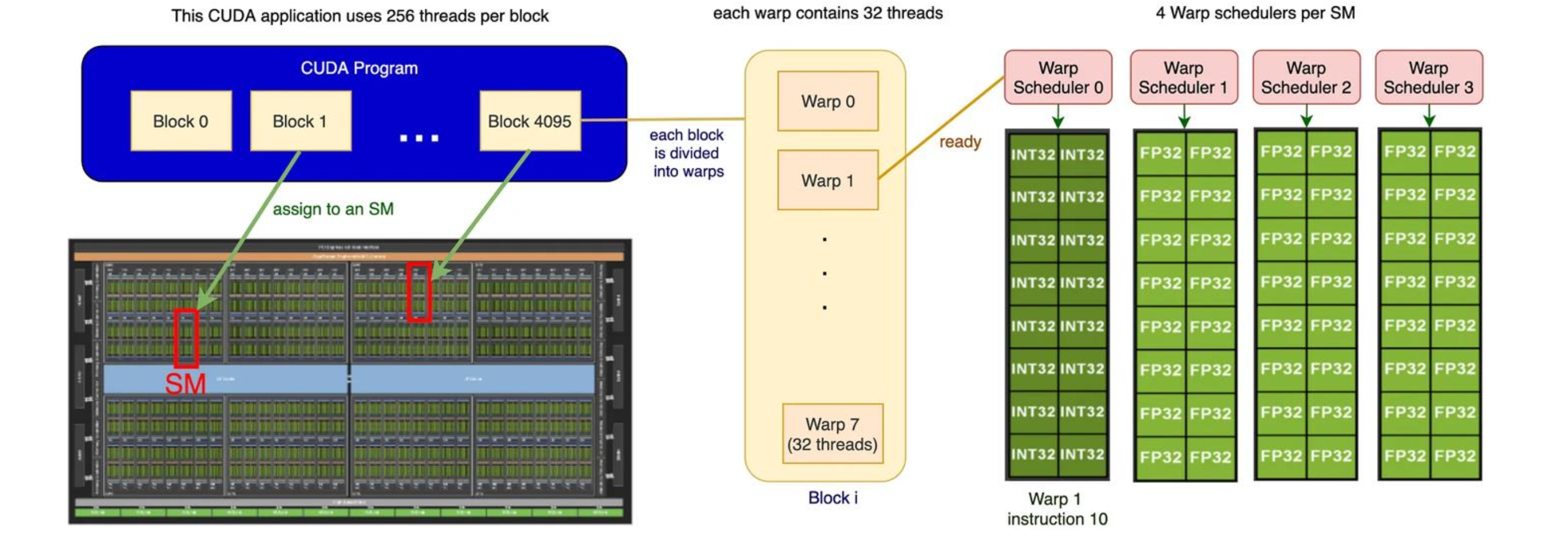
如下图所示,GPU 有很多流式多处理器 SM 单元, SM 单元是执行编程模型中的“Block”的执行载体,其具备控制单元,根据资源允许,一个 SM 会并发驻留多个 Block 块;单个 SM 由很多流式处理器 SP 构成,每个 SP 代表编程模型中的一个“thread”,SPs 在不同的数据上执行相同的指令。
GPU 内存架构
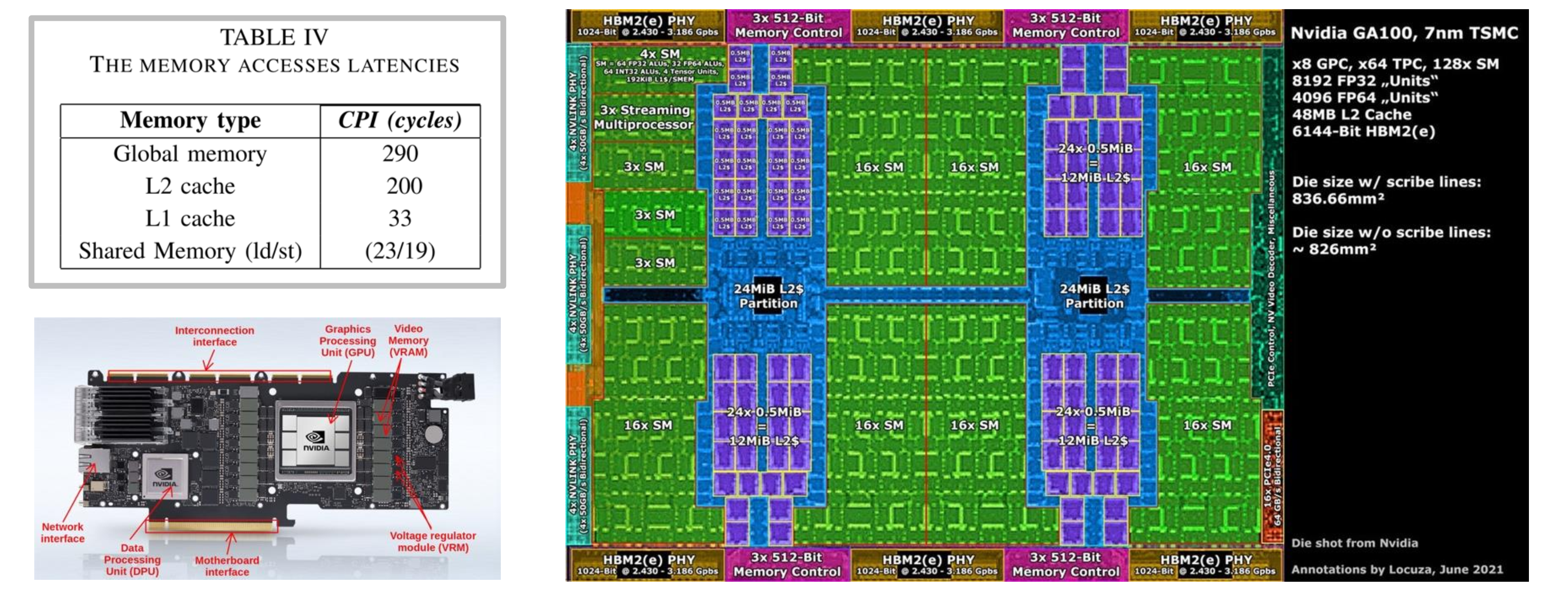
一言以蔽之,内存离 SM 越近,它的速度就越快,延迟就越小。L1 和共享内存在 SM 内部,其访存延迟最小;L2 缓存在片上,其延迟是共享内存的 10x;全局显存是 GPU 核心邻近的存储芯片,其延迟最大。
GPU 的执行模型
GPU 的执行模型分为 Block、Thread、Warp 三个级别:
- Block 由多个线程束 Warp 组成,具有独立的显存
- Warp 由 32 个连续的线程组成,线程以线程束为单位进行调度
- Thread 实际的执行单元,线程对不同的数据执行相同的指令,即所谓的 SIMT 模型
GPU 编程模型的优势
- 很容易扩大规模——堆叠 SMs 即可
- 得益于 SIMT 模型,容易(?)编程
- 线程是轻量化的,切换线程的开销很小
一些趋势
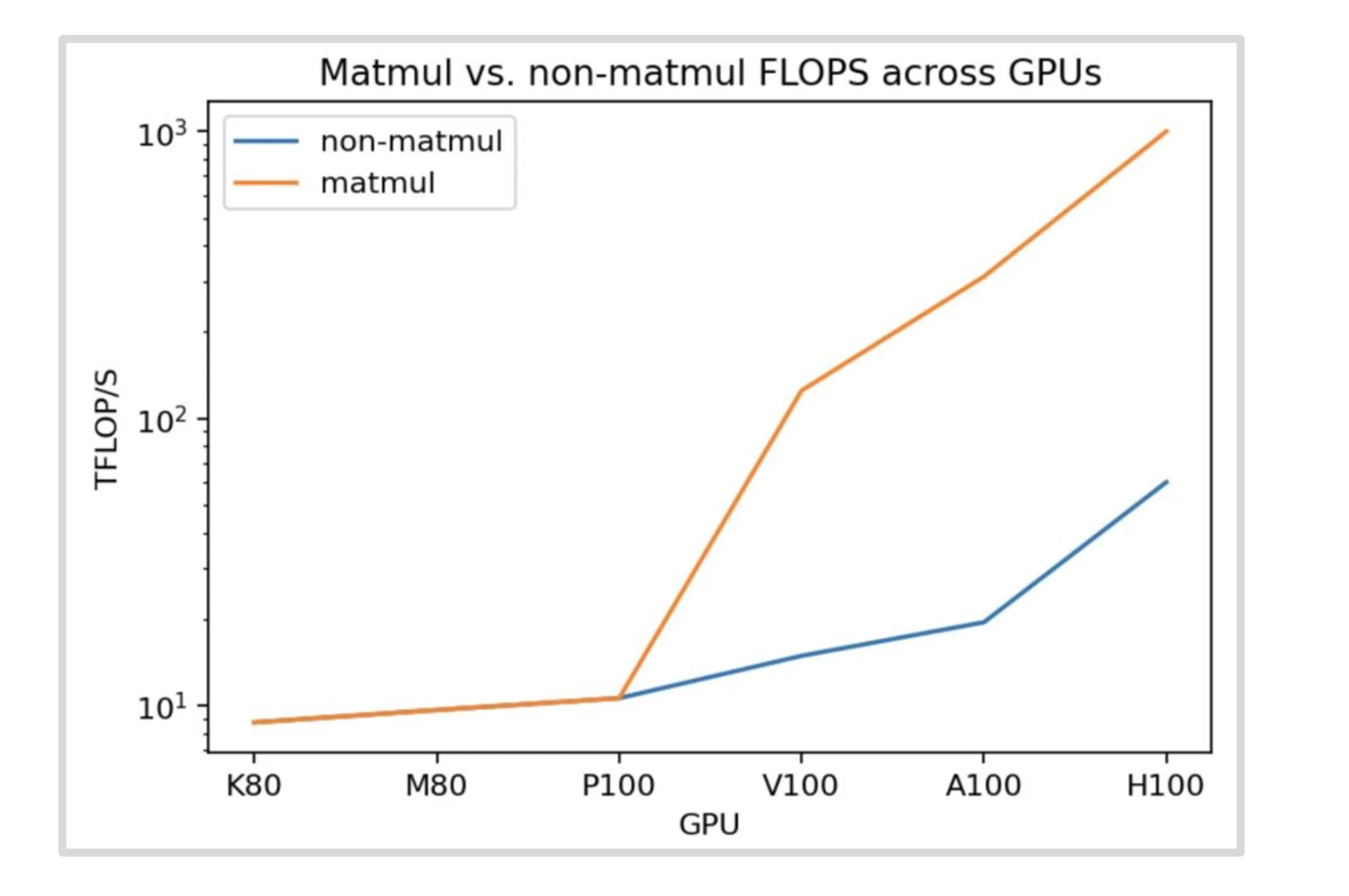
- GPU 算力在矩乘上做了高度特化
从下图可以看出,NVIDIA 的 GPU 在发展过程中矩乘和非矩乘的算力提升幅度差异巨大。这意味着我们在构造神经网络时要尽可能使用基于矩乘的算子才能获得最大的硬件收益。
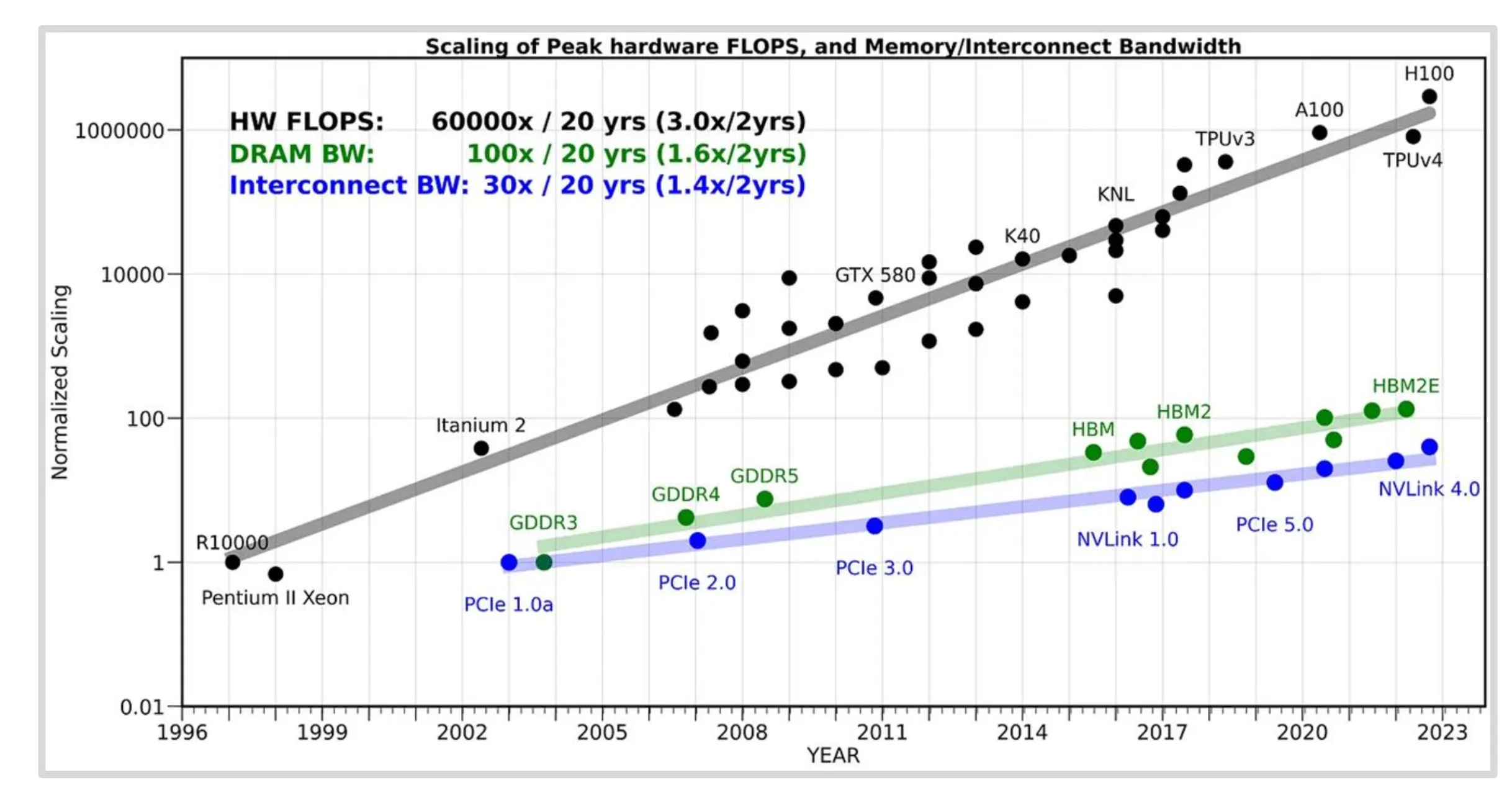
- 算力的发展速度快于通信和存储
让机器学习任务在 GPU 上跑的更快
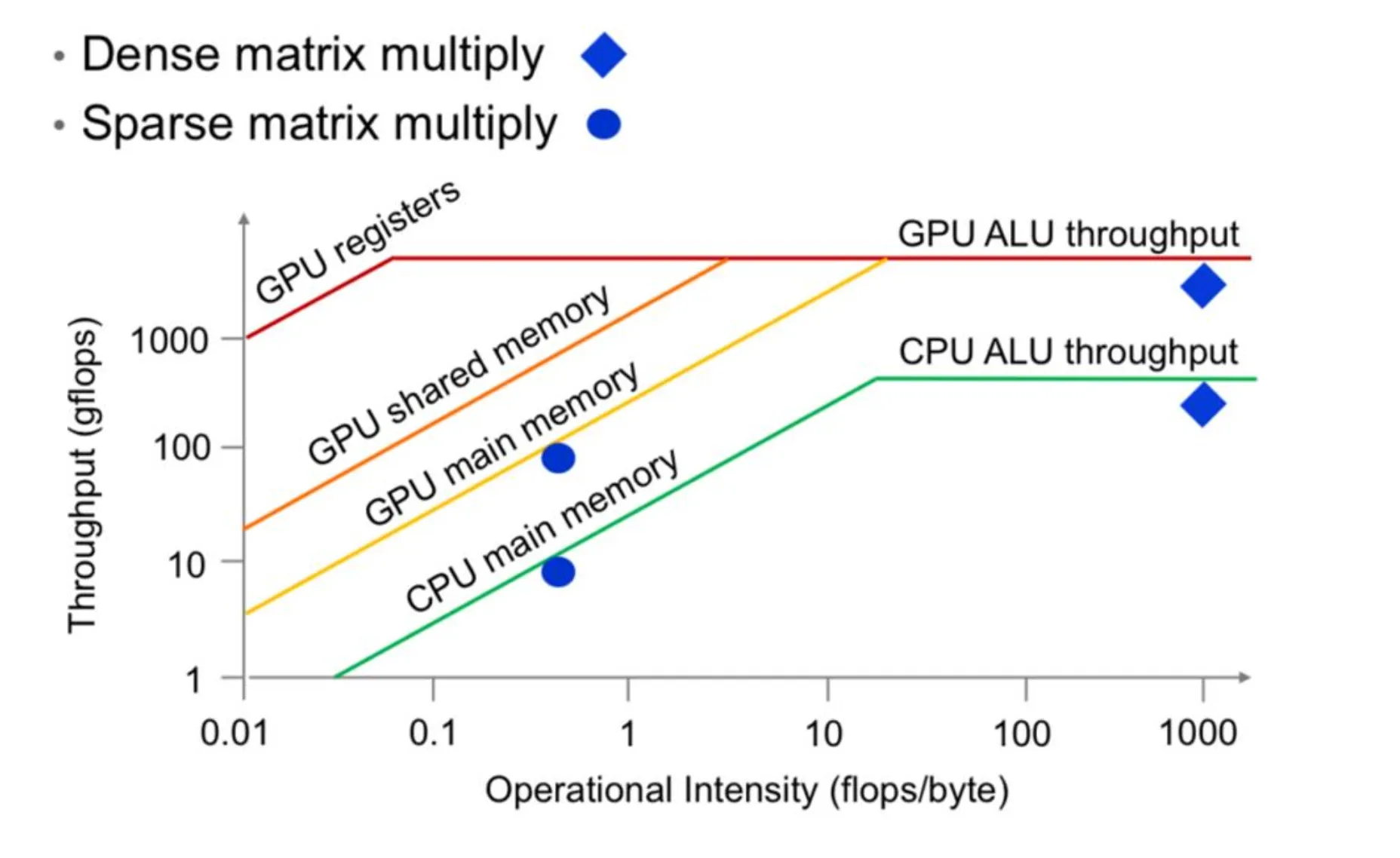
Roofline 模型
以计算强度为横轴,吞吐量为纵轴,可以绘制出形如屋顶的曲线,这条曲线可以显示不同计算密度下性能的瓶颈。在上升阶段,瓶颈在于访存;在水平线上,瓶颈在于计算。
技巧零:控制流分歧
GPU 上同一个线程束内执行相同的指令,因此在控制语句中如果同一个线程束中的条件值不一样,那么这些线程就会依次进入所有必要的分支,这相当影响这个线程束的执行性能。这点在之前学习 PMPP 时有提到,参阅:Programming Massively Parallel Processors A Hands-on Approach 4th Edition 学习笔记 Part 1 | 周鑫的个人博客
这是本节中唯一一个与内存无关的技巧。
技巧一:低精度计算
低精度的数据类型占据的空间更小,随之而来的就是更高的计算密度。如下所示,低于 ReLU 算子,将数据类型从 FP32 切换为 FP16,能够将计算密度提升一倍。

低精度存在舍入导致的精度问题,因此在 Tensor Core 中矩乘会使用全精度的累加器来计算,从而同时获得低精度低内存带宽和高精度计算精度的收益。
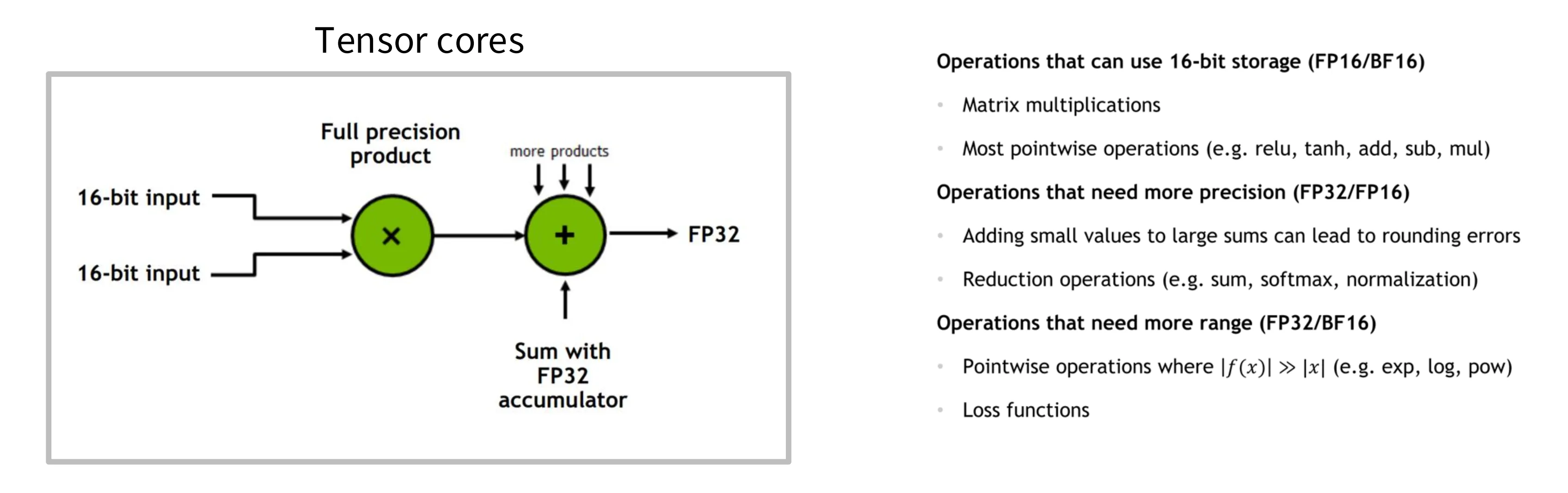
技巧二:算子融合
如下图左,当有很多算子的时候,如果不做算子融合,就需要反复对同一块数据(作为输入输出)进行搬运。此时,可以将多个小算子融合成一个大算子,一次搬运,多次计算,只在必要时才对数据进行搬运。
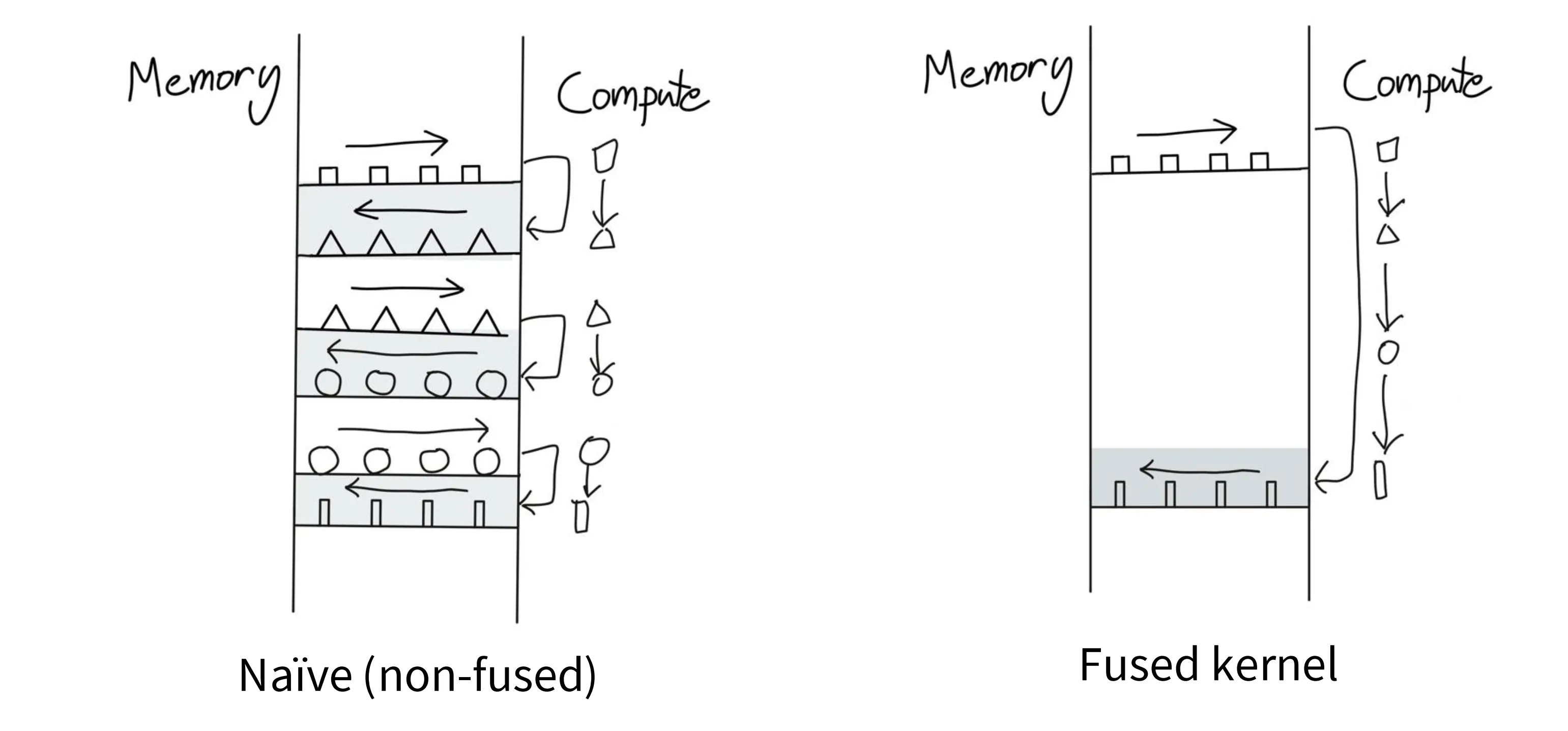
技巧三:Recomputation
在依次前向计算过程中,我们需要保存每一层的输出以便在反向中计算梯度。使用重计算技术我们可以在求反向过程中重新计算一遍前向的激活值,从而减少数据搬运。如下所示,一个三层的 Softmax 的前向 + 反向需要 8 次访存,应用重计算后只需要 5 次,访存需求减少 38%。这个技术与模型训练过程中减少显存占用的重计算是同一个技术,只是二者的出发点不同,一个为了加速,一个为了节省显存。
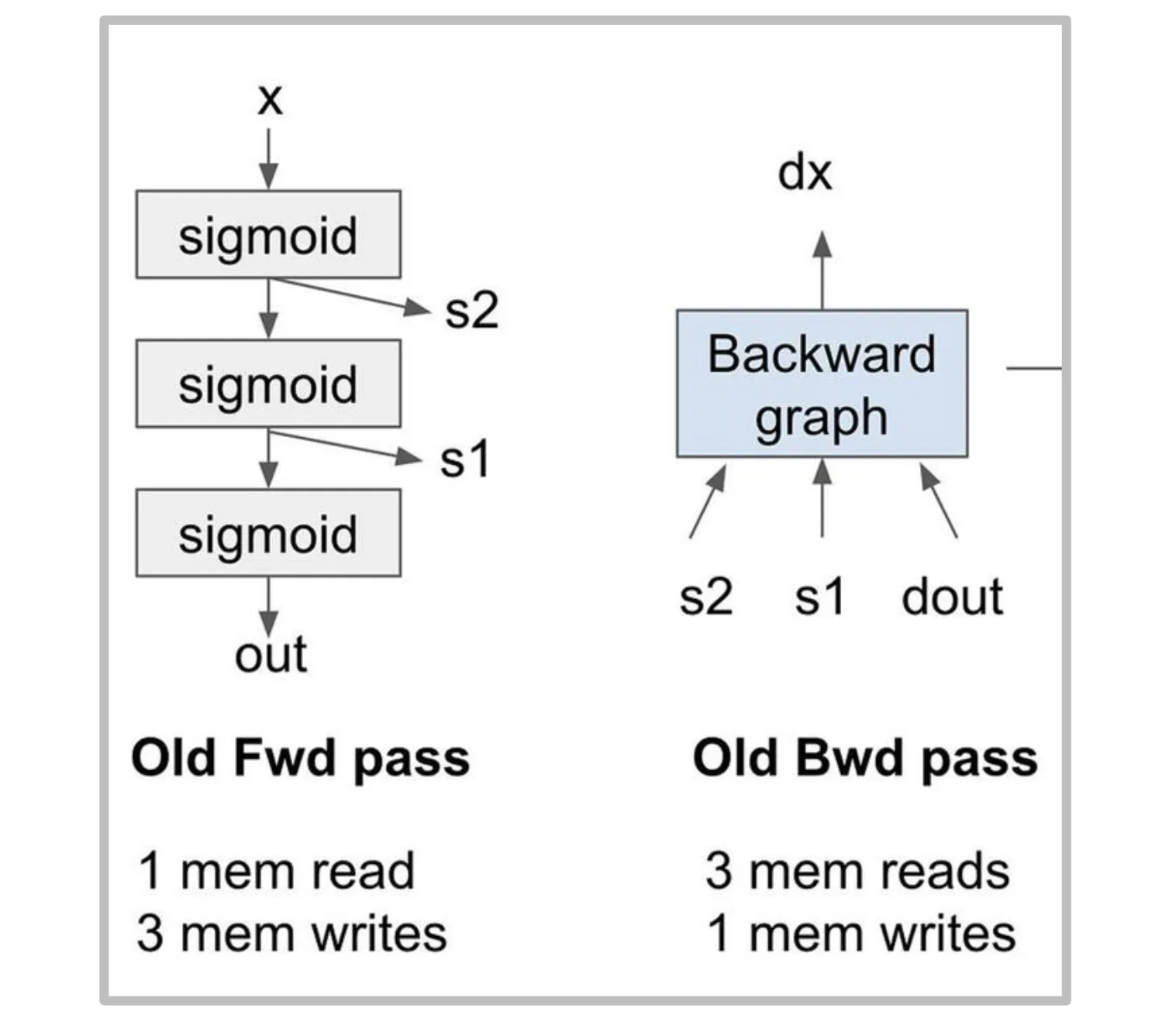
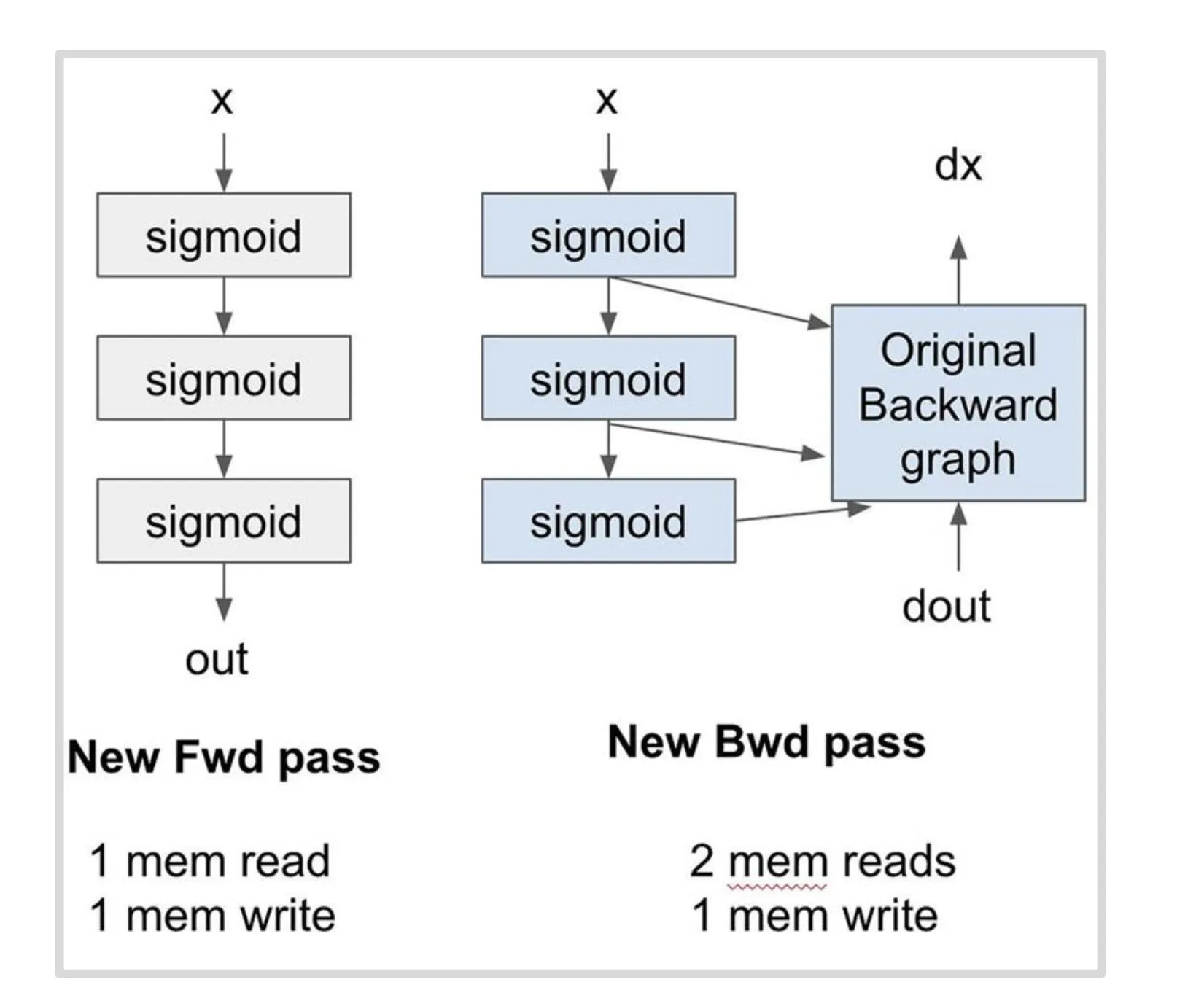
技巧四:内存合并访问
这也是一个在 PMPP 中重点介绍的技术:Programming Massively Parallel Processors A Hands-on Approach 4th Edition 学习笔记 Part 1 | 周鑫的个人博客。
DRAM 的物理结构决定了其支持突发访存,即当访问某个位置的元素时,其周围连续的元素也会被一起读取。
为了充分利用突发访存的特性,CUDA 会自动将线程束中的多个线程连续的访存指令转换为突发访存指令,即如果线程束中 0-31 号线程的同一个访存指令访问的目标是全局内存中连续的 32 个位置,则该访存指令将通过突发访存来实现。具体请参考之前的学习笔记。
技巧五:分块
分块的动机是减少对全局内存的重复访存,将这些重复访存合并对片上内存的重复访问。
如下图所示,在朴素的矩阵实现中,每 P(0,0) 这个元素会被多个线程反复访问,并且这些线程访问的模型也不是合并访问的模式,这会大大降低执行效率。
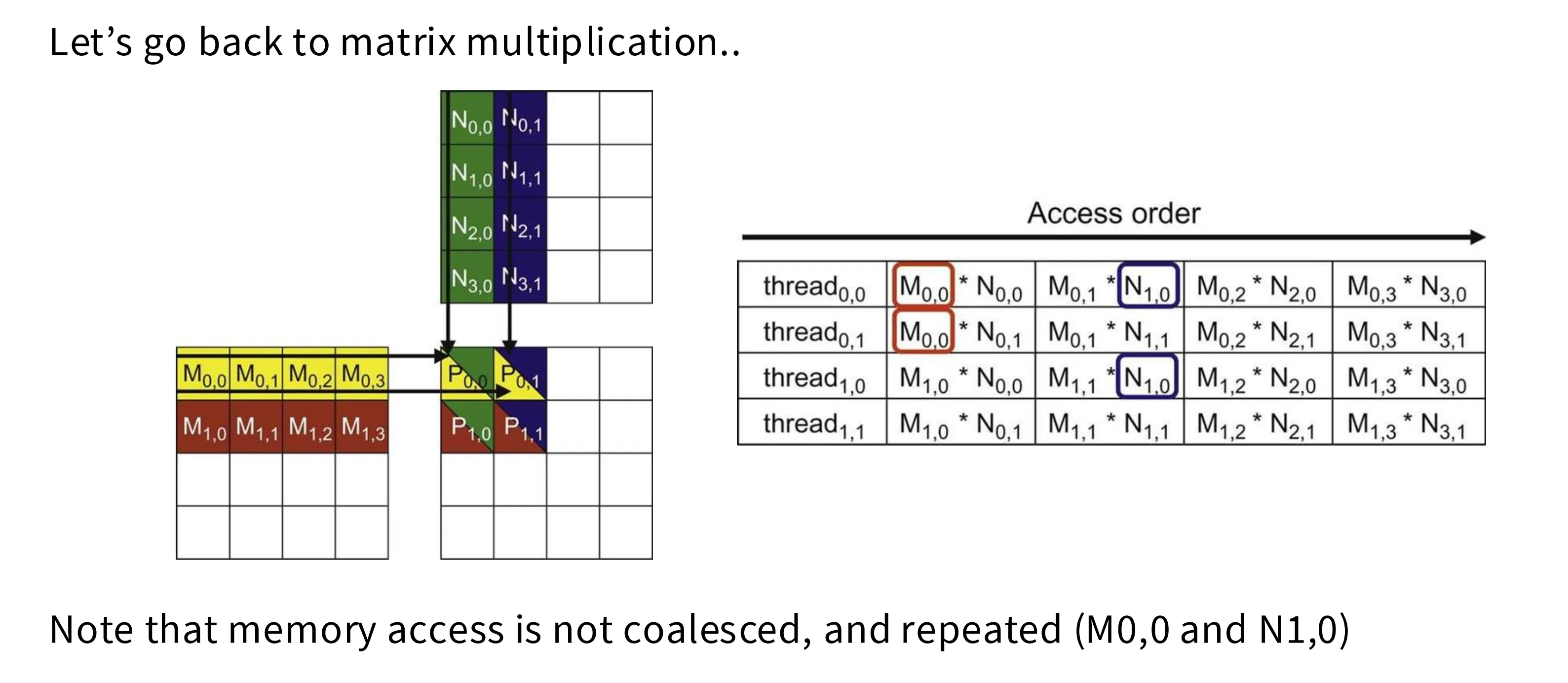
将输入矩阵按照 2x2 分块以后,就可以将计算设计的小块使用合并访问的访存模式提前加载到共享内存中,并重复利用
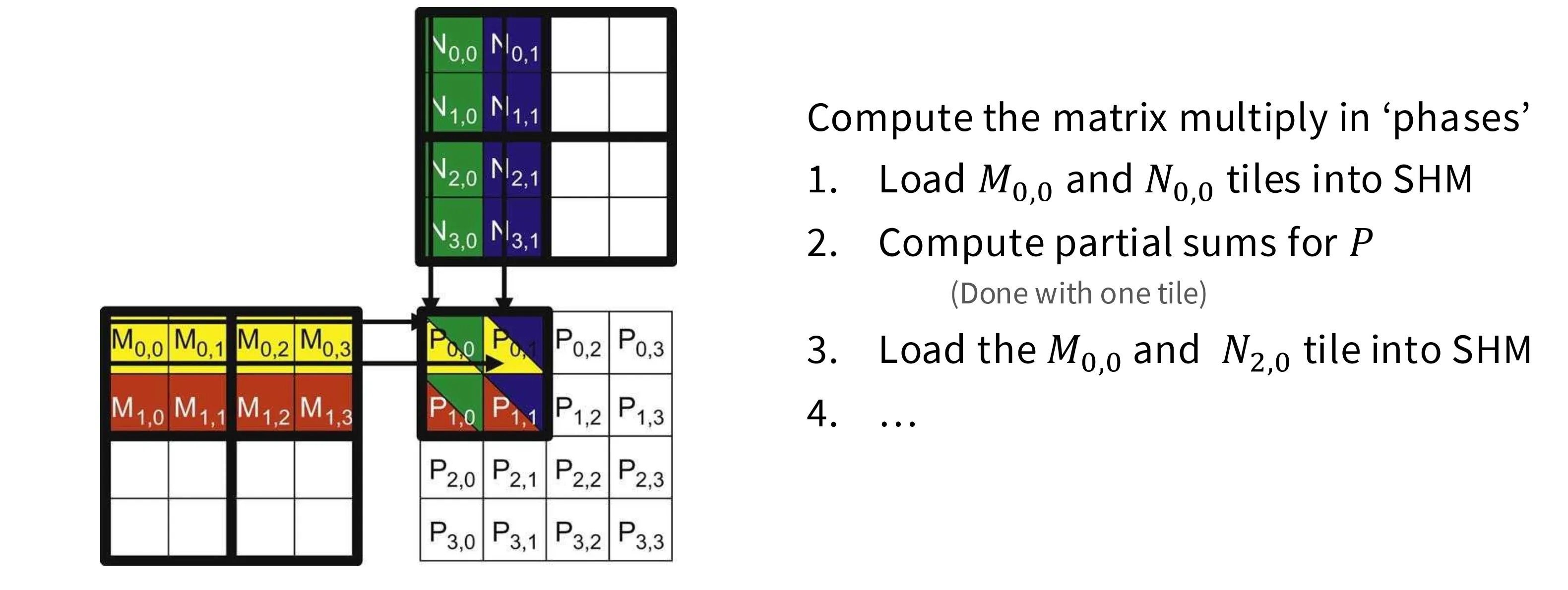
如果我们按照步长 T 对 NxN 的矩阵分块,在非分块的情况在每个元素要被加载 N 次,而在分块的情况下每个元素只要被加载 N/T 次,这是 T 倍的加速比,相当可观。
在实际应用中,分块大小可能无法被原张量形状整除,这就会导致资源利用低效。分块大小受到很多因素的约束:
- 内存合并访问
- 共享内存大小
- 原始张量的形状
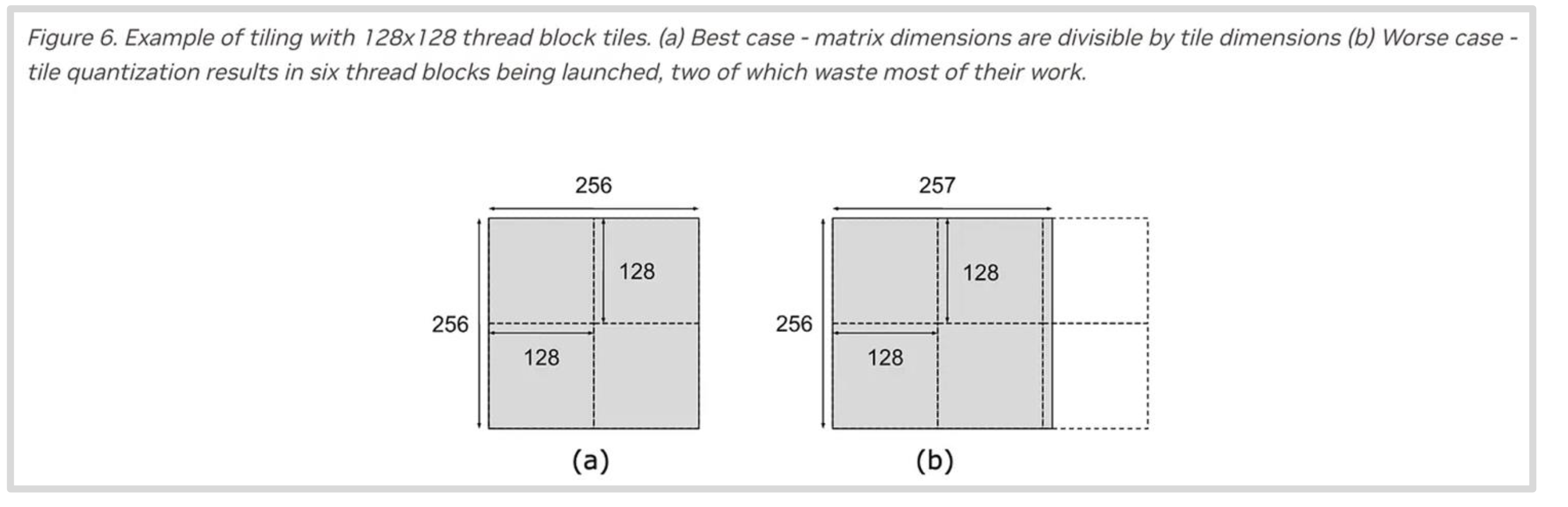
分片的另一大挑战是内存对齐,如果输入张量的形状不是很完美,分片后每个 Block 需要访问的数据横跨两个不同的突发访存块中,那么访存次数相比对齐的情况就会加倍。这类问题的解决方案是通过 padding 手段将其补全为一个内存对齐的布局。
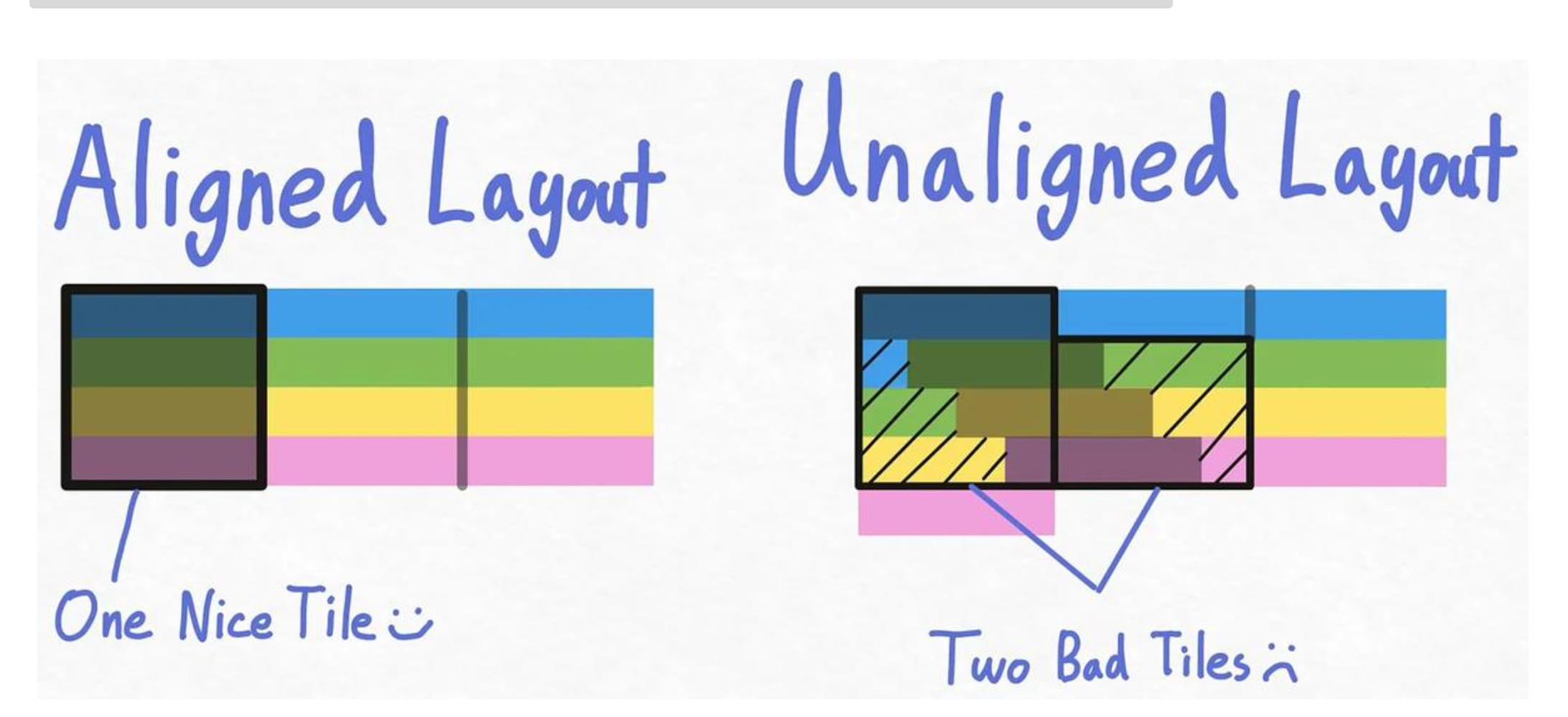
矩乘性能图
下图展示了矩阵乘法计算吞吐量随矩阵形状的变化情况,本节将应用前面所讲的理论对此进行解释。
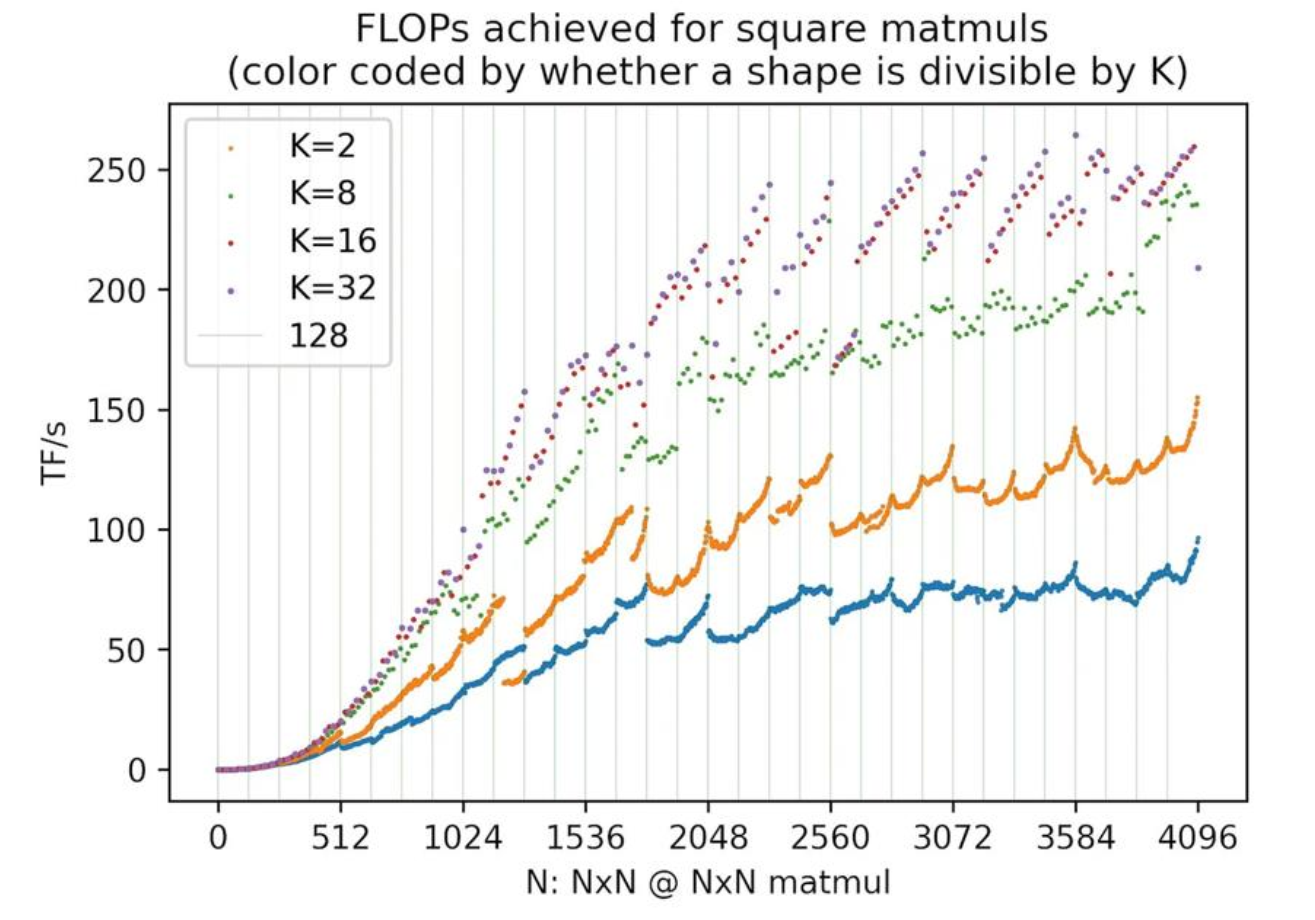
- 在 size 增加的前期,性能瓶颈在于访存,此阶段吞吐量随计算密度的提升而提升;在后期呈现出波浪线的阶段,性能瓶颈在于计算,即 roof line 的水平阶段。
- 曲线之间的性能差异来自内存对齐和内存合并访问
- 在波浪线阶段,以 K=2 为例,从 1792 到 1793 出现了陡峭的性能下降。这是因为 GPU 在计算矩乘是一般以 256x128 进行分块,1792 需要 98 个 SM,而 1793 需要 120 个 SM,A100 一共只有 108 个 SM,无法一轮全部执行所有的 120 个 Block 所以性能陡峭下降。
FlashAttention
FA 通过使用分块和重计算技术,显著提升了 Attention 的计算速度并降低了对 HBM 的访存需求:
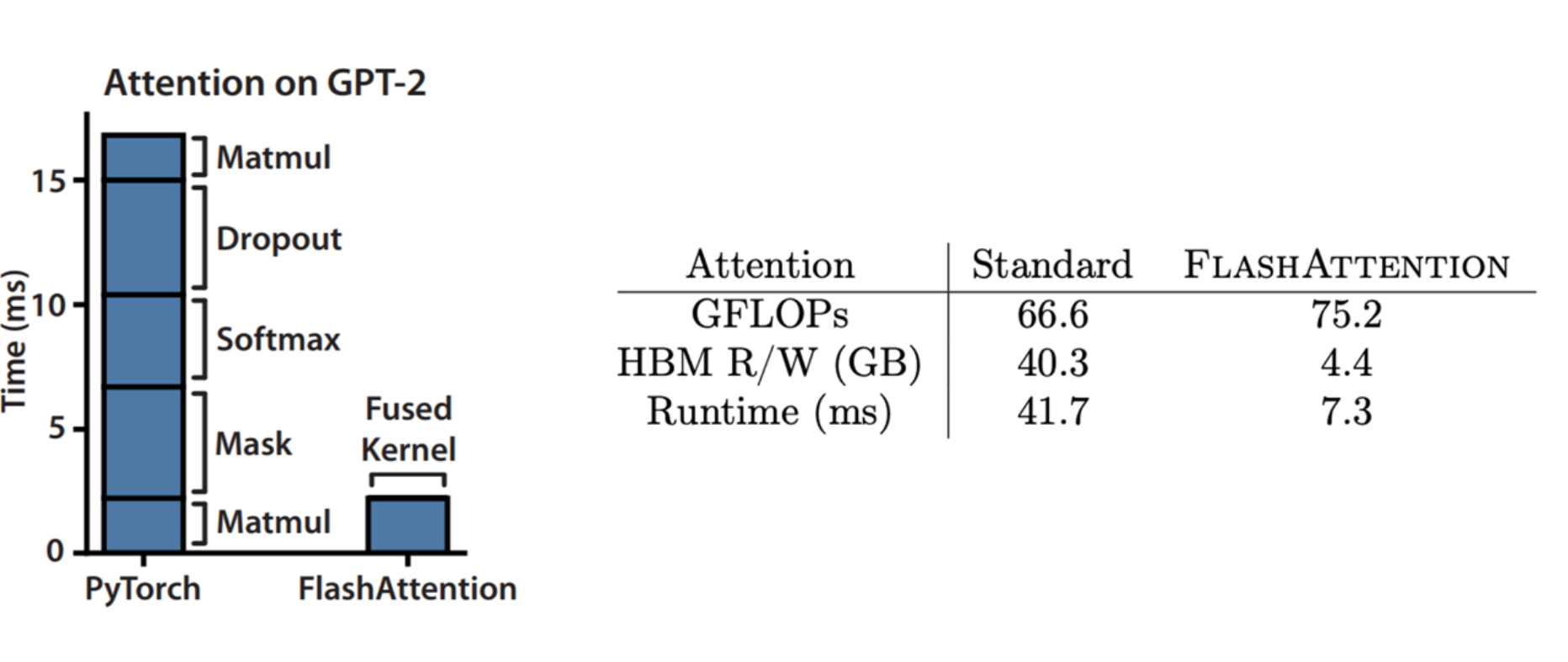
分块一:对 KQV 矩乘分块
第一个分块操作是对 KQV 之间的矩阵乘法进行分块计算,这是之前讲过的常规操作:
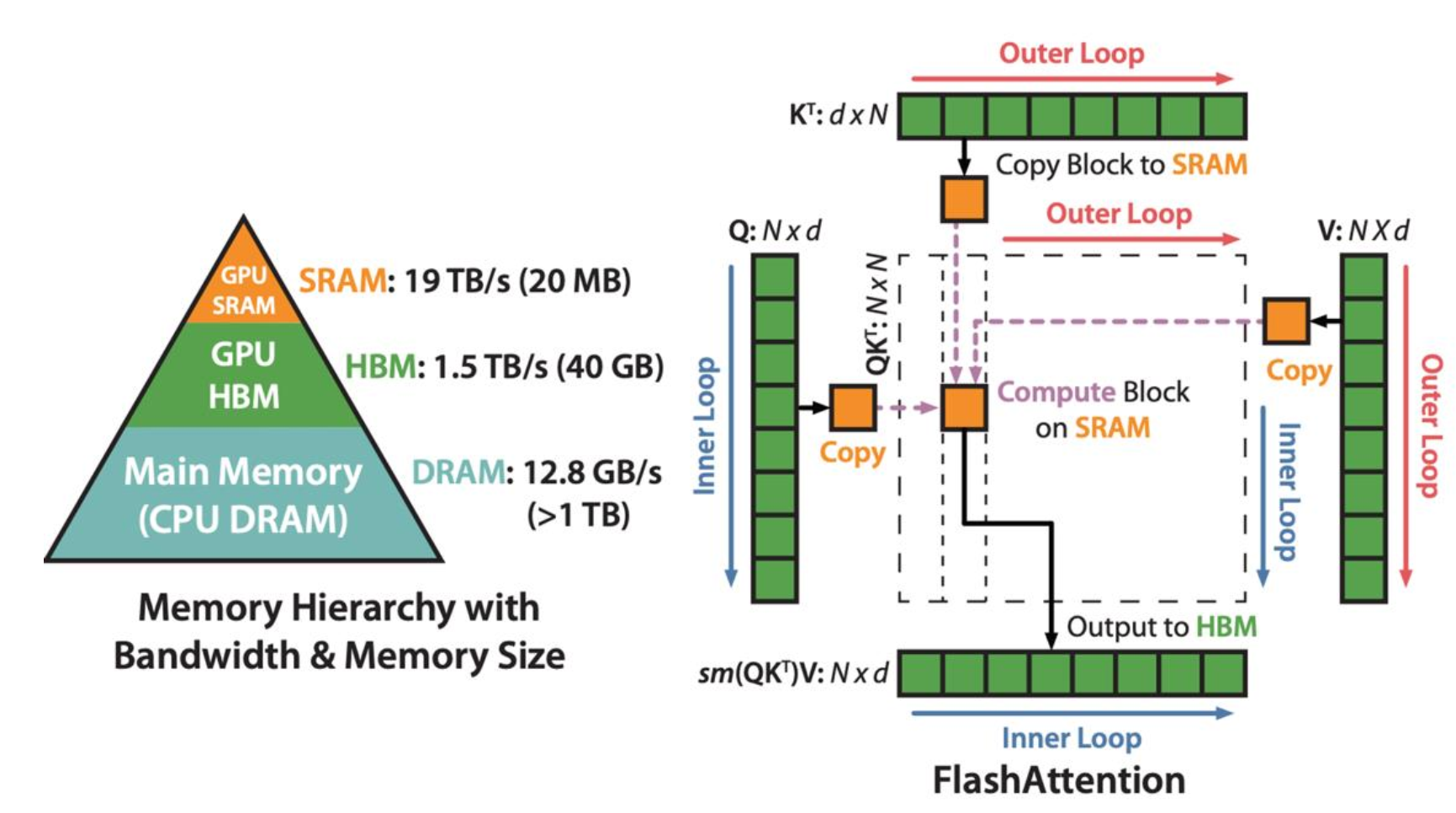
分块二:Softmax
标准的 Softmax 需要至少对数据进行三次遍历:
- 遍历所有数据,找到最大值
- 再次遍历数据,计算分母
- 第三次遍历数据,计算结果
其痛点在于这个过程无法分块,需要先统计出全局最值之后才能计算最后的结果。
而 Online Softmax 则引入了一个技巧,在不知道全局最值的情况在边扫描数据,边维护 Softmax 统计量。具体来说,设我们处理到第 $j-1$ 个元素,当前的局部最大值是 $m_{j-1}$,当前的局部和是 $d_{j-1} = \sum_{k=1}^{j-1} e^{x_k - m_{j-1}}$。现在进来一个新的元素 $x_j$,需要进行两个操作:
- 更新最大值:新的最大值 $m_j = \max(m_{j-1}, x_j)$。
- 更新分母和:我们需要把旧的 $d_{j-1}$ 修正到基于新最大值 $m_j$ 的尺度上。
利用指数运算性质:$e^{x - m_{new}} = e^{x - m_{old} + m_{old} - m_{new}} = e^{x - m_{old}} \times e^{m_{old} - m_{new}}$,所以新的和 $d_j$ 等于:
基于上述数学变换,我们可以在每个 tile 内计算局部最大值和求和值,最后再讲结果合并以修正误差。
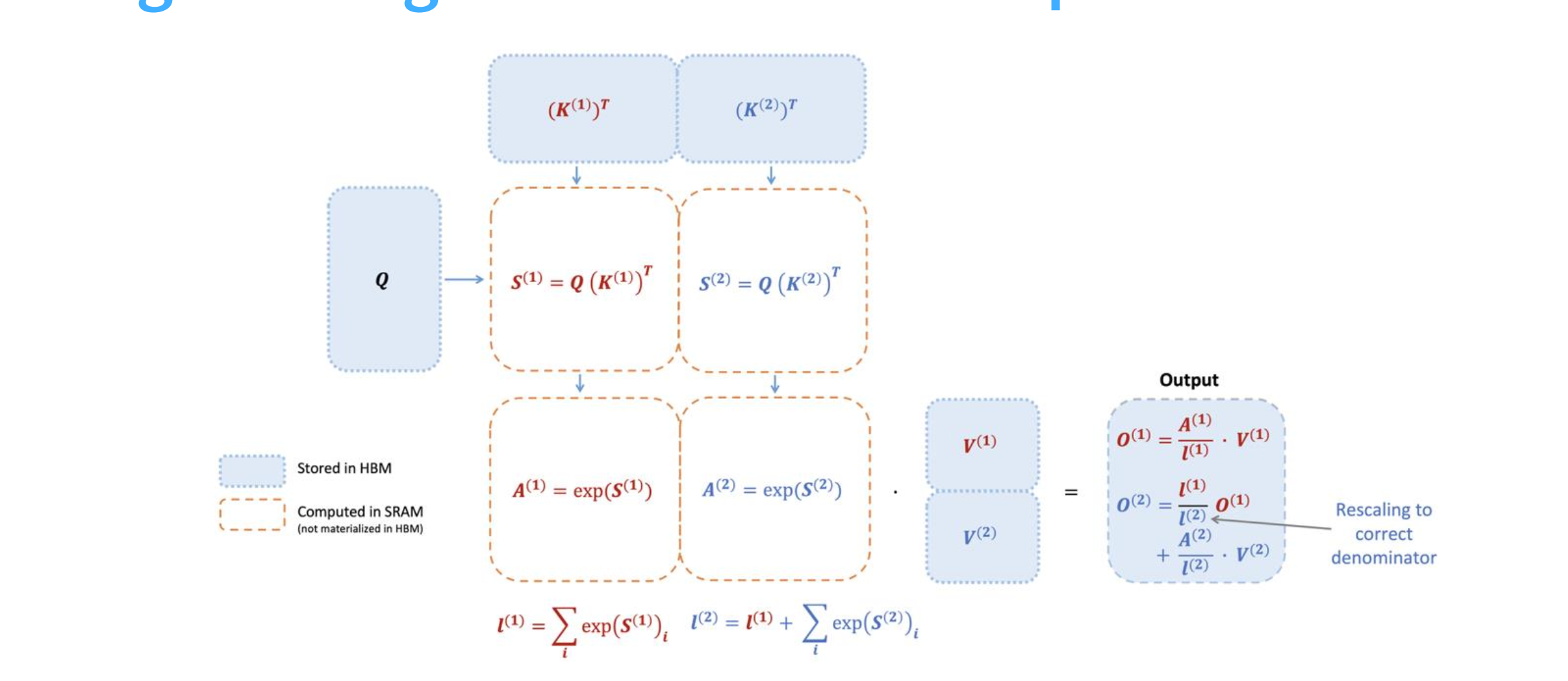
FA
下图展示了 FA 的计算过程,首先对 QK 进行分块矩阵,算完立刻做 Online Softmax,并得到一组输出,最后再做一次修正得到最终的结果。这里只是理论介绍,忽略了很多细节,后面 Lab 2 中应该是需要手搓一个 FA 的。