TL;DR 本讲 CS336 系列笔记的第四讲。本讲梳理了 MoE 架构利用稀疏激活实现“高效扩参”的核心机制，并结合 DeepSeek 系列模型的演进路线，重点解析了细粒度专家、共享专家及无辅助损失负载均衡等策略，如何解决大规模训练中的路由坍塌与稳定性难题。

引入

什么是 MoE

MoE 模型指的是将 Transformer 架构中的 FFN（MLP）模块替换为多个稀疏的 FFN 模块（专家），前向计算时每次只稀疏激活一部分专家，由此实现在不增加计算量的情况加增加模型参数。
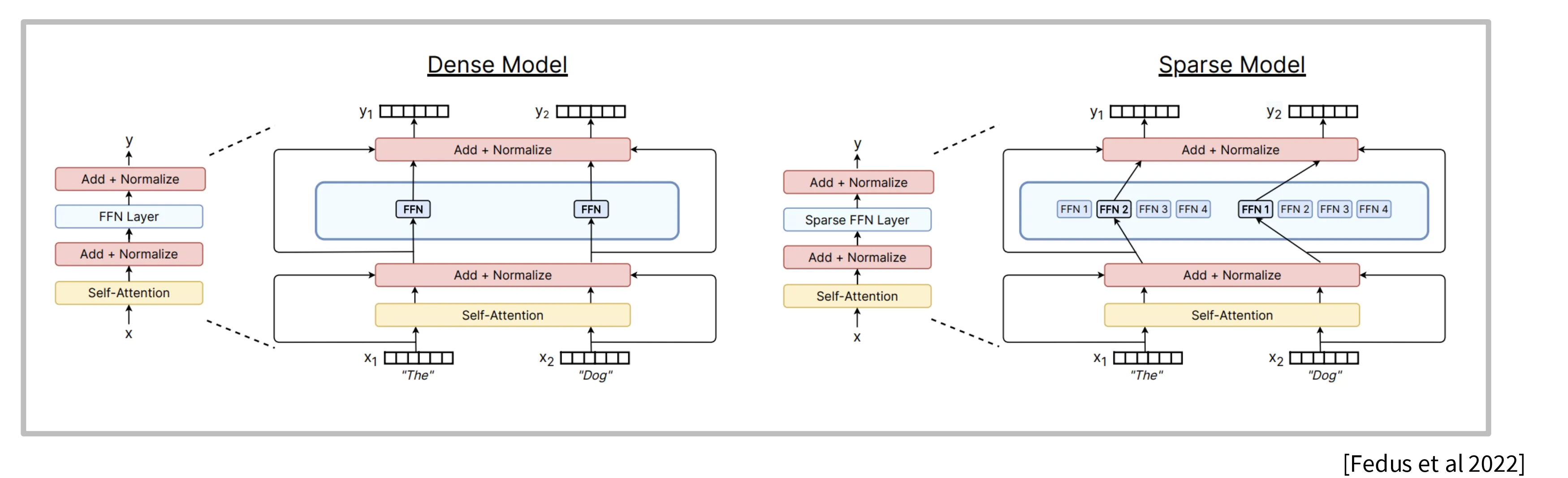
image.png

由于 MoE 架构同计算量在模型参数更多，最终学习到的模型的性能也更好，因此 2025 以来主流模型均转向了 MoE 架构。

当然，天下没有免费的午餐。MoE 的代价是整个模型尺寸变得更大，需要更多的存储空间，以及在并行化方面带来了更大的系统复杂度。

为什么 MoE 变成主流

  • 相同的计算量下，参数越多，模型性能越好。
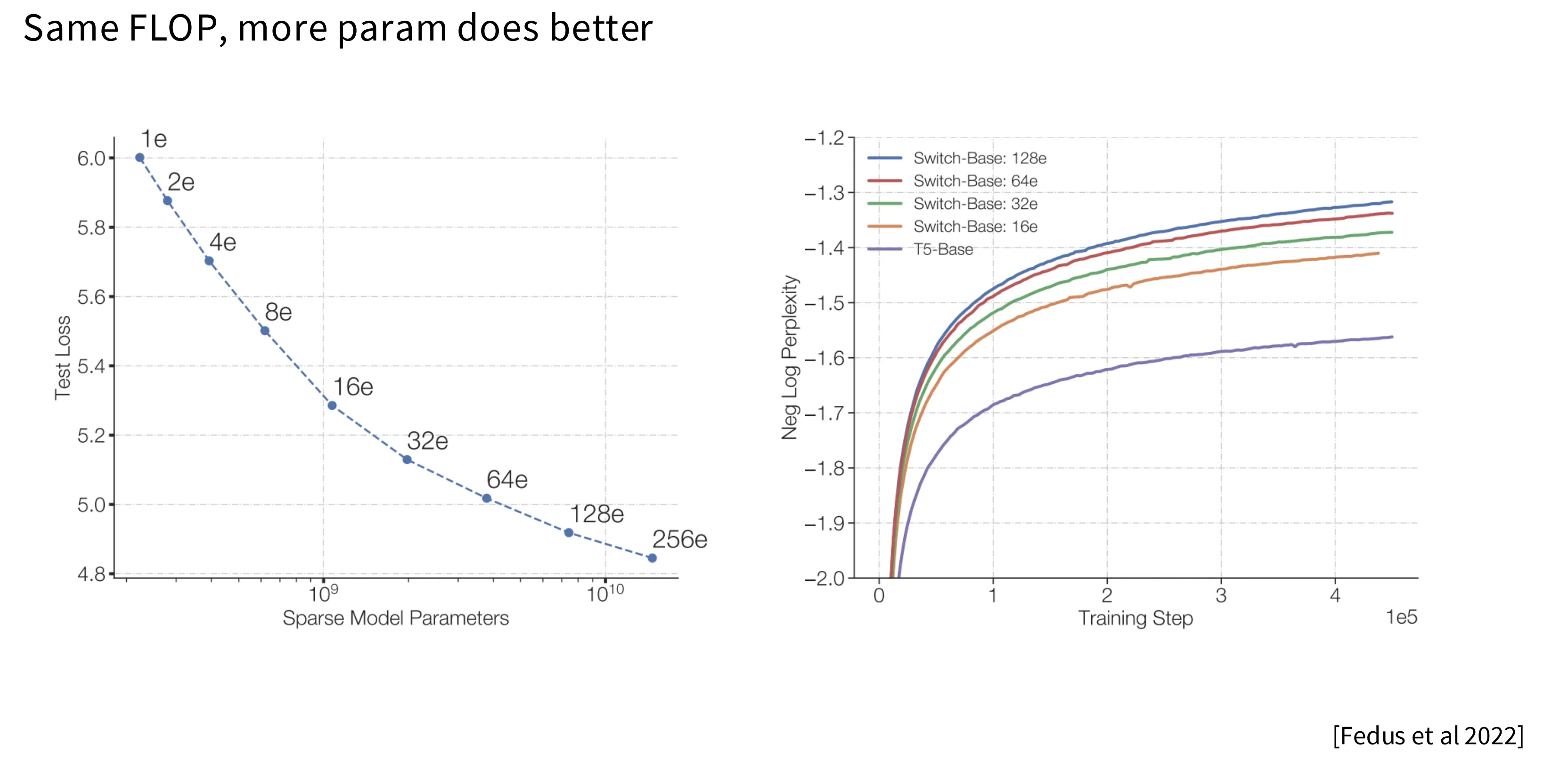
    image.png
  • MoE 训练更快。相比 Dense 架构，MoE 架构达到相同的 loss 只需要 1/7 的时间。
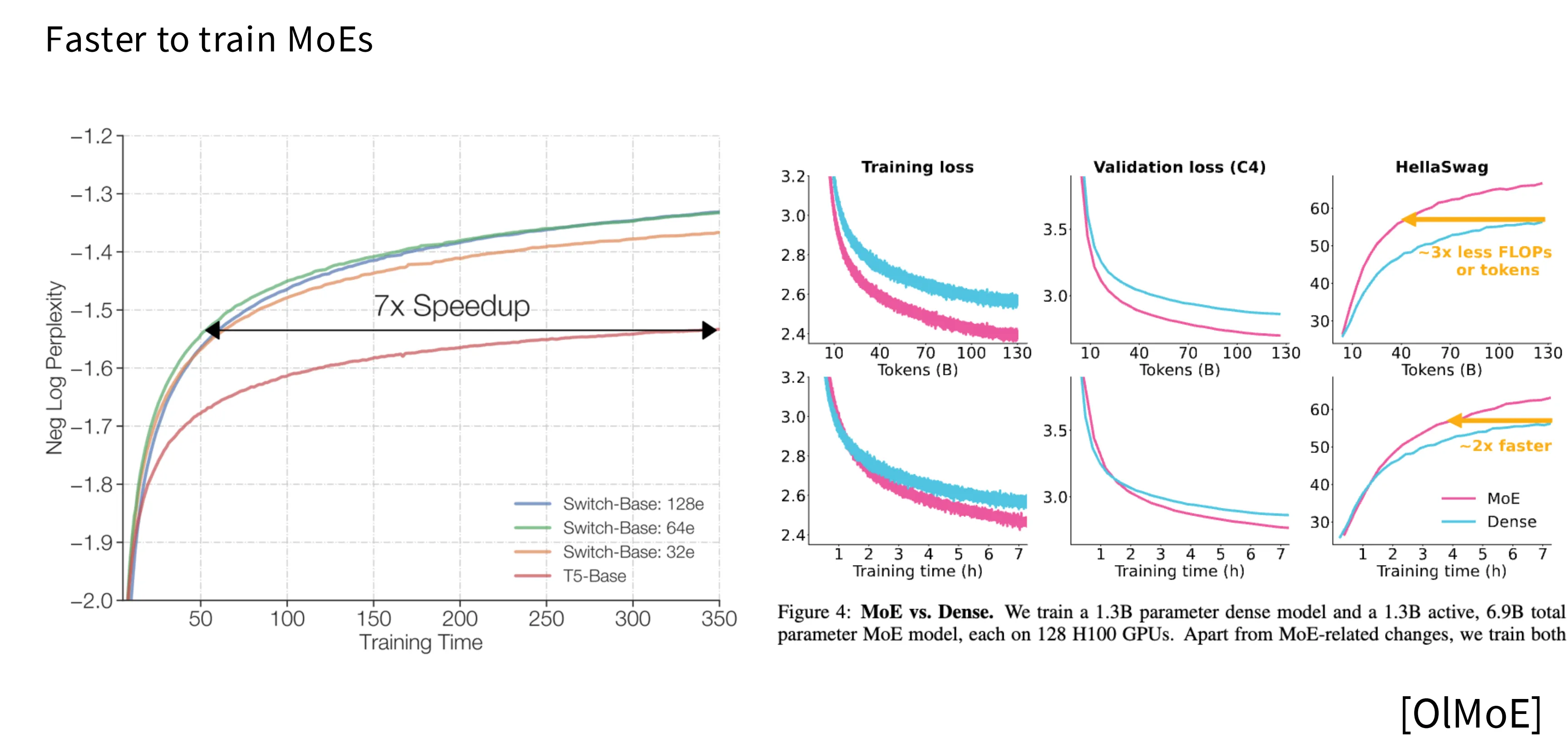
    image.png
  • 天然适合并行化。将 MoE 的不同专家部署到不同的设备上是一个很自然的想法。

MoE 的局限

  • 依赖于基础设施建设
    MoE 模型尽管在计算方面有优势，但是模型本身很大，这就要求训练团队需要有一套强大的基建能够支撑起 MoE 模型在训练过程中对于多硬件、多数据、高度并行化的需求，这对于中小团队来说是很困难的。

  • 训练过程依赖经验且不稳定
    MoE 的路由过程是不可微分的，并且路由策略的选择对训练结果影响巨大。因此相比稠密模型其训练过程更容易出现不稳定性，这对开发者的经验和技巧提出了更高的要求。

架构

通常 MoE 指的是下图左边的使用 MoE 替换 Transformer 中的 MLP 层，也有工作尝试使用相同思路将 MHA 替换为 MoE 的版本，但是这并不主流，并且此类模型的训练难度更大。
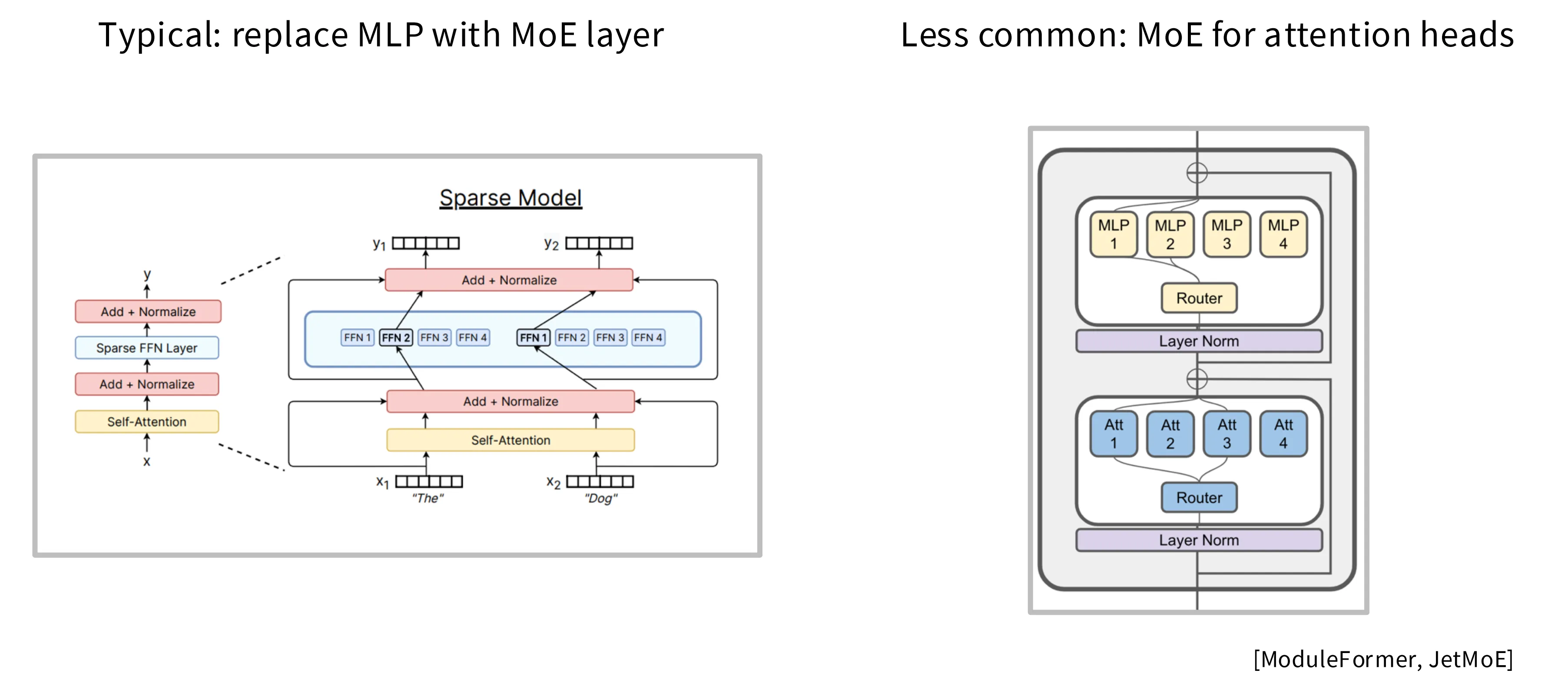
image.png

MoE 的变种

MoE 的各类变种可以归结为三类：路由算法、专家数量和损失函数。

路由算法

总览

路由算法指的是决定每个 token 去往哪个专家的路由机制。可以归结为三类：

  • token 选择专家：以 token 为主体，每个 token 独立挑选最匹配的专家
  • 专家选择 token：以专家为主体，每个专家从所有输入中挑选最匹配的 token
  • 通过全局优化路由：全局角度最优地分配 Token 到专家的任务，通常涉及复杂的数学优化问题
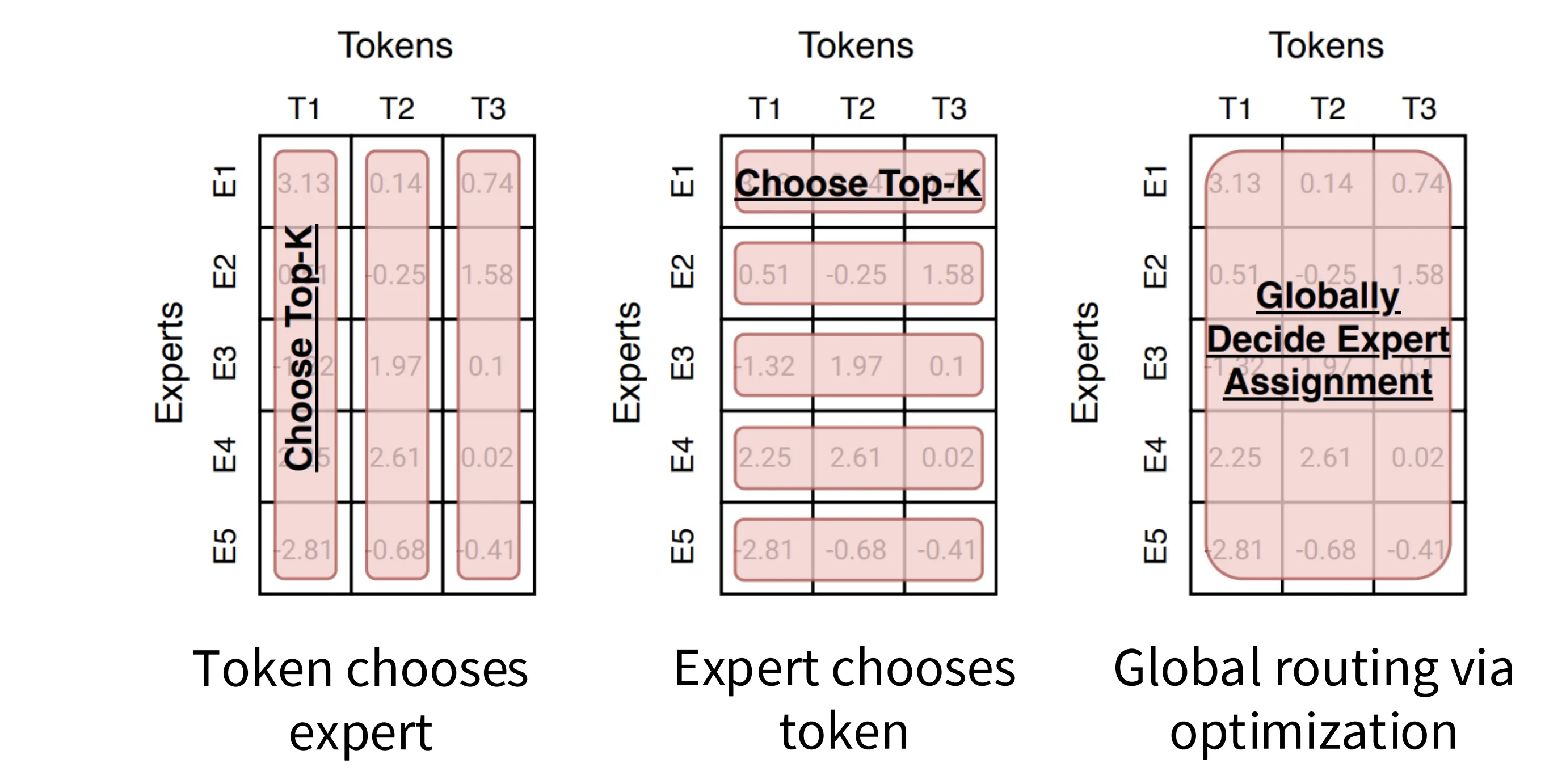
    image.png

常见算法

常见的路由算法是 Top-k 和哈希算法，后者使用一个哈希函数将不同的 token 映射到专家，常常作为 baseline 来评估其它路由算法。
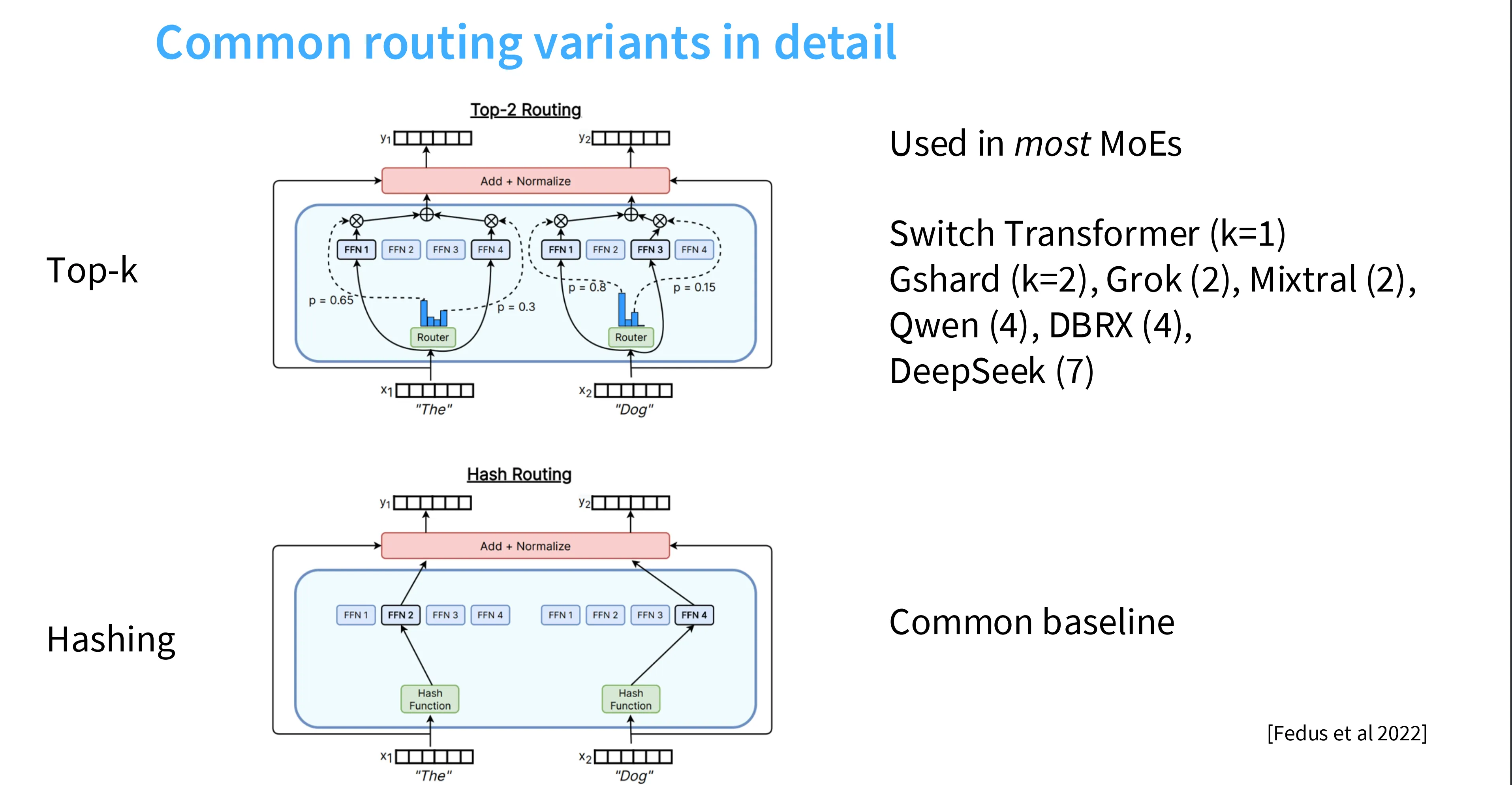
image.png

Top-K 算法

如下图所示（从下往上），在 Top-K 路由算法中，有一个可学习的参数 e，首先将输入 u 与 e 做内积，得到二者相似度，对相似度做 Softmax 得到每个专家的分数，然后过滤出前 k 个专家作为门控，再根据每个专家的分数对每个（前 k 个）专家的输出做加权求和。
image.png

Fine-grained Expert Segmentation 、Shared Expert Isolation

国产大模型在专家路由架构方面有两个技术趋势。下图 (a) 是传统的 Tok-2 路由算法；(b) 是细粒度专家分割，即将单个专家规模缩小一半，专家总数增加一倍，激活专家数增加一倍，总计算量没有增加，但是专家数的增加能够带来更好的性能；(c) 是共享专家隔离，引入一个始终被激活的专家，从可解释性的角度来说，这个专家可以解决知识冗余的问题，即这个始终被激活的专家负责记忆那些“大家都得会”的知识。
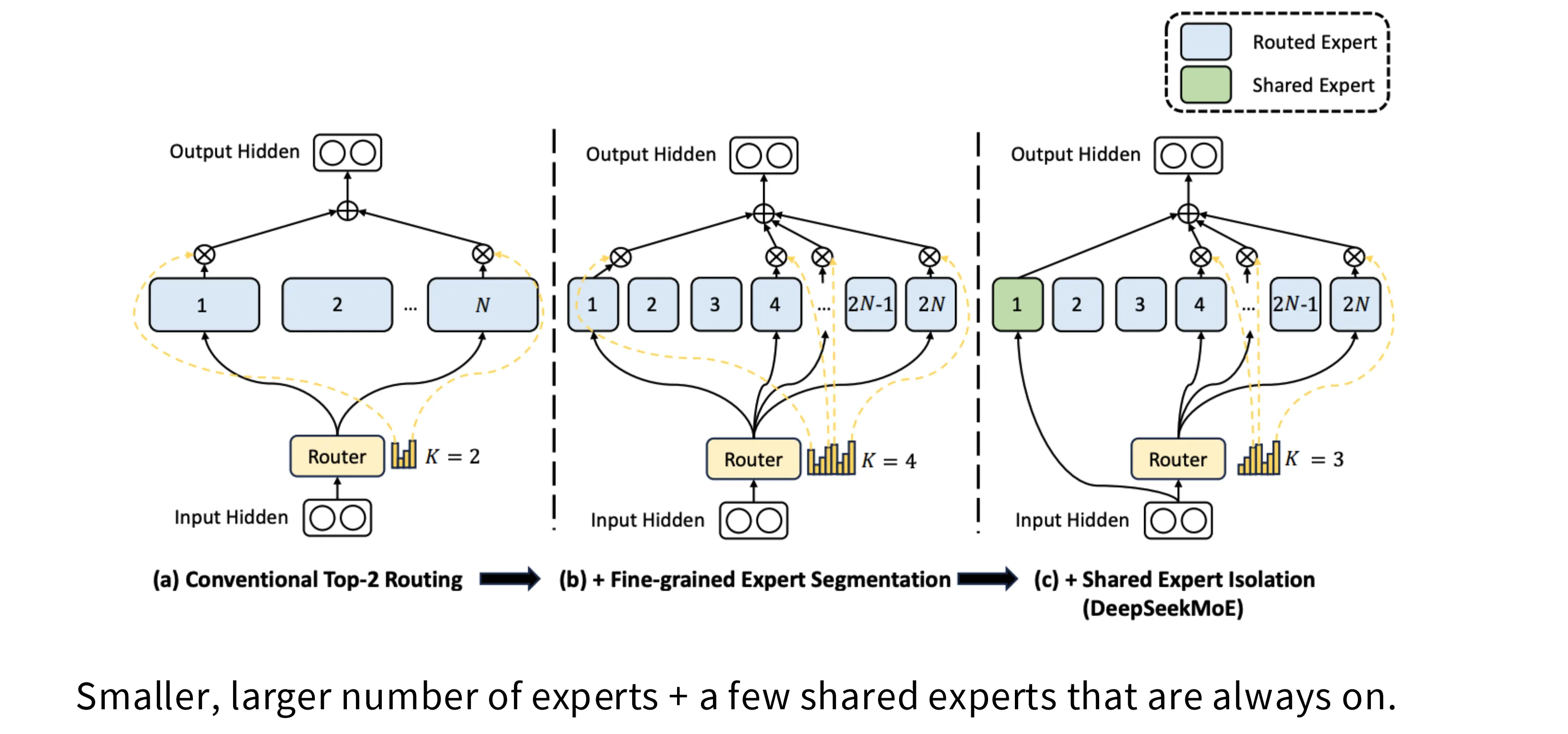
image.png

从 DeepSeek 技术报告中的消融实验可以看出，上述架构的演进确实能够提升模型的性能。
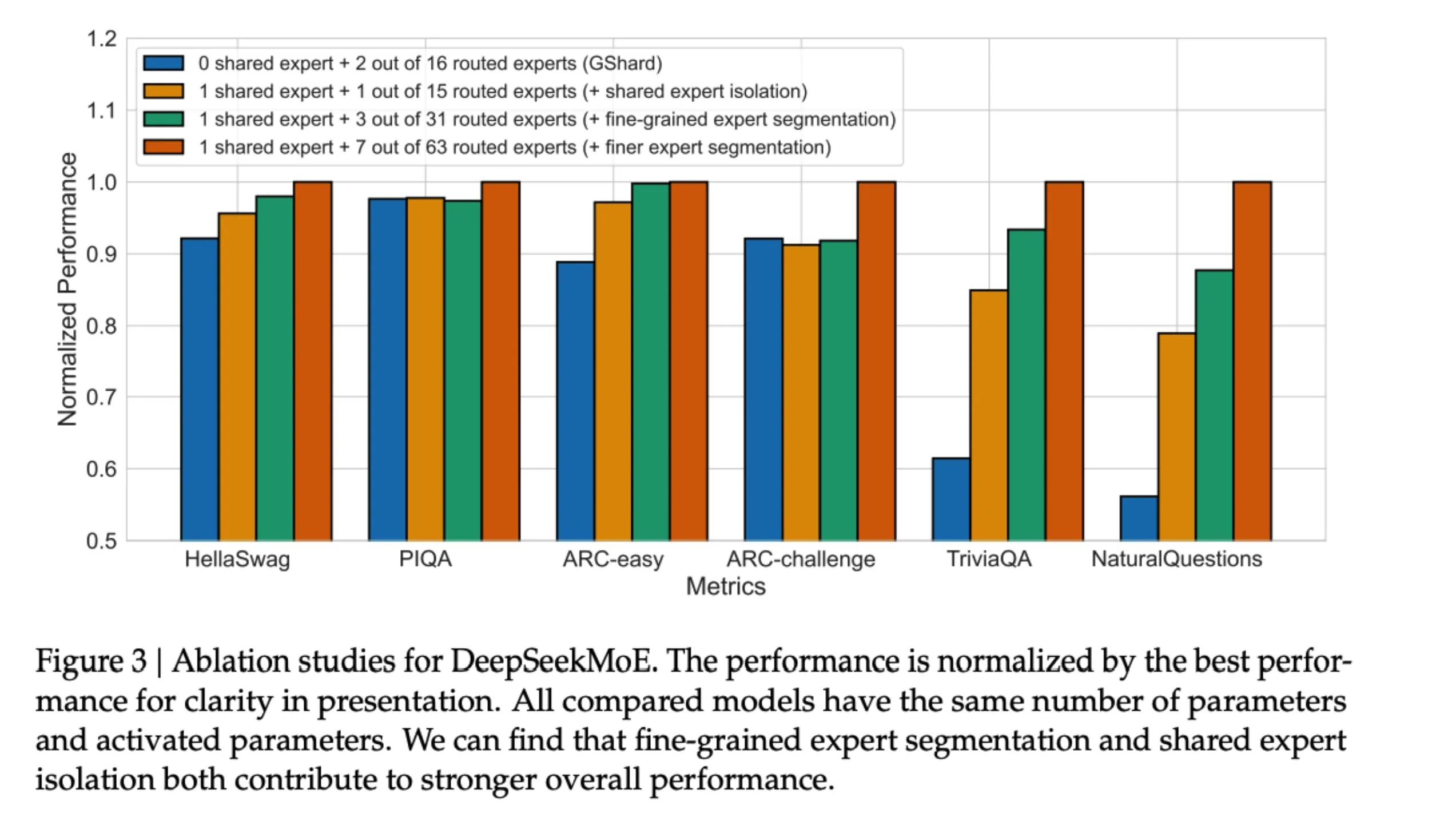
image.png

训练 MoE

梯度实际上是可以顺着被选到的专家流动下来的。这里所谓的不可微分实际指的是只有被选到的专家才有梯度，但是选不到的专家很容易陷入饿死的状态，即强者越强，弱者越弱，永远得不到更新。

专家路由是一个离散不可微分的过程，对此有三种解决方案：

  • 强化学习
  • 随机扰动
  • 启发式负载均衡损失

强化学习

强化学习可以对离散变量进行建模，理论上其完美适配这个问题，但是实验数据表明这个方法相比其它方案、甚至相比基线模型其性能优势并不显著，但是引入强化学习的同时还带了梯度的不确定性和整体复杂度的显著提升，因此目前没有工作在大规模训练上使用强化学习解决 MoE 的训练的问题。
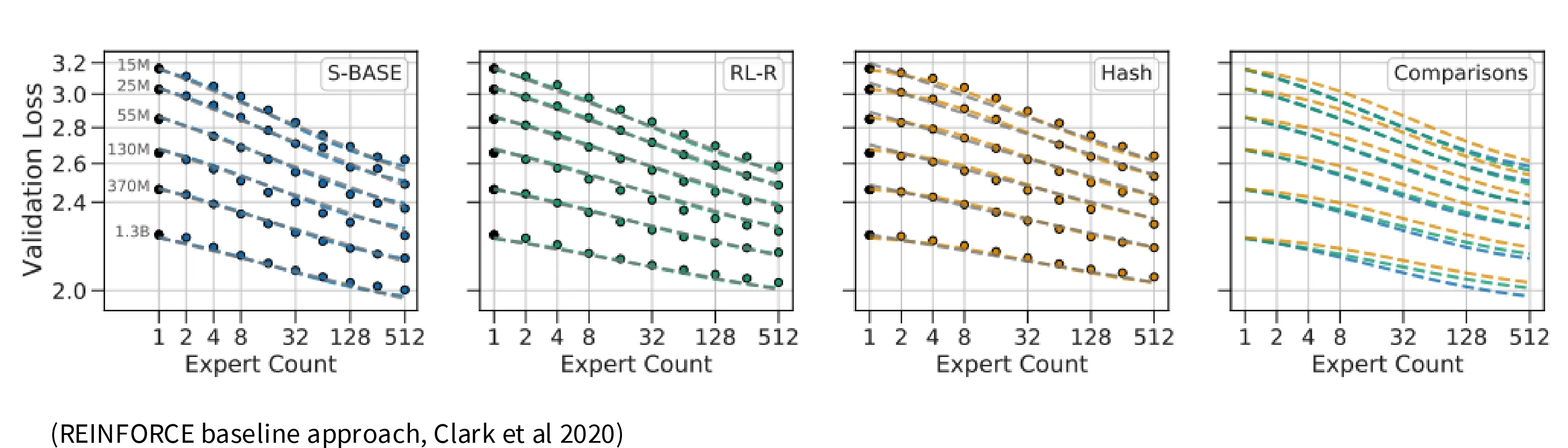
image.png

随机扰动

随机扰动这个方案通过在路由的分数中加入正态分布的噪声和一个可学习的线性层控制整体噪声的幅度。随机性因素的加入使得模型有着更好的鲁棒性，但是此类方案在 LM 后期也由于其潜在的不稳定性被抛弃，业界投向效果更好的启发式方法。

image.png

启发式负载均衡损失

这是在 Switch Transformer 中提出的方案，引入一个辅助的损失函数，这个函数是对每个专家的 $f_i$ 和 $P_i$ 的积求均值得到，其中 $f_i$ 表示专家 $i$ 在一个 batch 中实际被选中的概率，$P_i$ 表示专家 $i$ 在路由算法中被分配到的概率总和的平均值。

image.png

引用自 Gemini 的答疑解惑：

为什么不直接优化 $f_i$ 使之趋向平均分布？
因为 $f_i$ 是由离散路由算法计算出来的，是一个不可微的值。

为什么不直接优化 $P_i$ 使之趋向平均分布？
因为 Top-K 算法只对数值的绝对排序敏感，只优化 $P_i$ 仍无法杜绝马太效应——只要模型让最强大的专家的分数略高于平均分布即可。

总结，这个 loss 设计得非常巧妙，它实际上是在说：如果一个专家实际上很忙（$f_i$ 大），那我们就惩罚它的预测概率（$P_i$），以此来减少它未来被选中的机会。

在 DeepSeek v1-2 中，还有一个结构类似的辅助损失函数，其作用是在设备之间实现负载均衡，将频率统计从按照专家统计改为按照设备统计即可：
image.png

如果没有负载均衡机制，可以看到模型的性能不如上了负载均衡的情况。此外，如果咩有负载均衡机制，只有两个专家被路由，其他专家专家都饿死了。
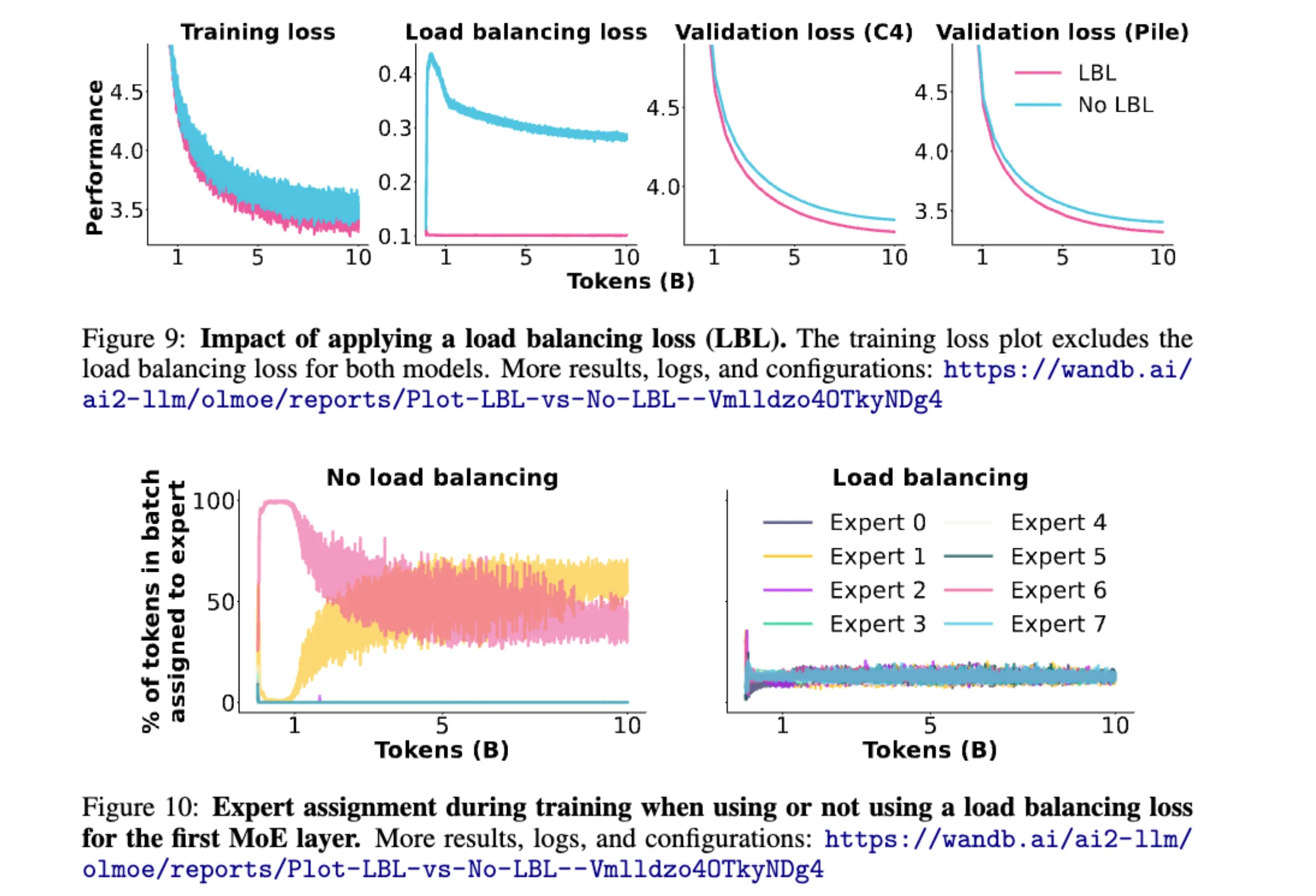
image.png

无需辅助损失的启发式负载均衡

在 DeepSeek V3 中提出了一种不需要引入辅助损失的负载均衡手段。其在 Softmax 计算得到的注意力分数中额外增加了一个偏置项，这个偏置项与这个专家的实际负载负相关，从而实现
image.png

MoE 的问题

随机性

当模型所在的卡无法容纳更多的 token 时，多出来的 token 会被丢弃，这在训练和推理阶段引入了随机性，使得模型的输出可能会在不同的 batch 之间表现不同。

稳定性

路由算法中的 Softmax 计算存在稳定性问题，尤其是在 BF16 下，一点数值扰动或者舍入可能对最终的输出有很大的影响。为此，需要在路由选择计算中采用 FP32 并在必要时引入上一讲中介绍的 z-loss 优化手段。

可以看到，z-loss 的引入可以有效抑制训练过程中损失函数的尖峰。
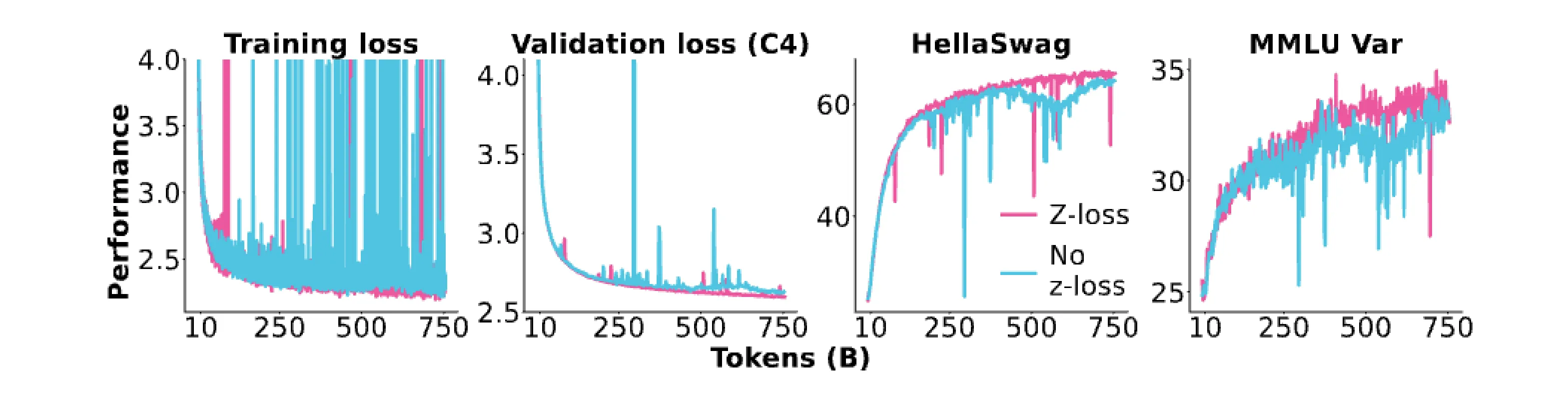
image.png

微调

MoE 模型在微调过程中很容易过拟合。一种解决思路是调整模型架构，在模型架构中交替使用 MoE 和 Dense 架构，在微调时只对 Dense 部分微调。另一种思路是大力出奇迹，增加数据量。

Upcycling

一种低成本训练 MoE 模型的方式是先训练一个 Dense 模型，然后将 Dense MLP 拷贝 n 份来构造出一个 MoE 架构，并以此为起点开始训练。通过这一方式可以高效地训练出一个 MoE 模型。
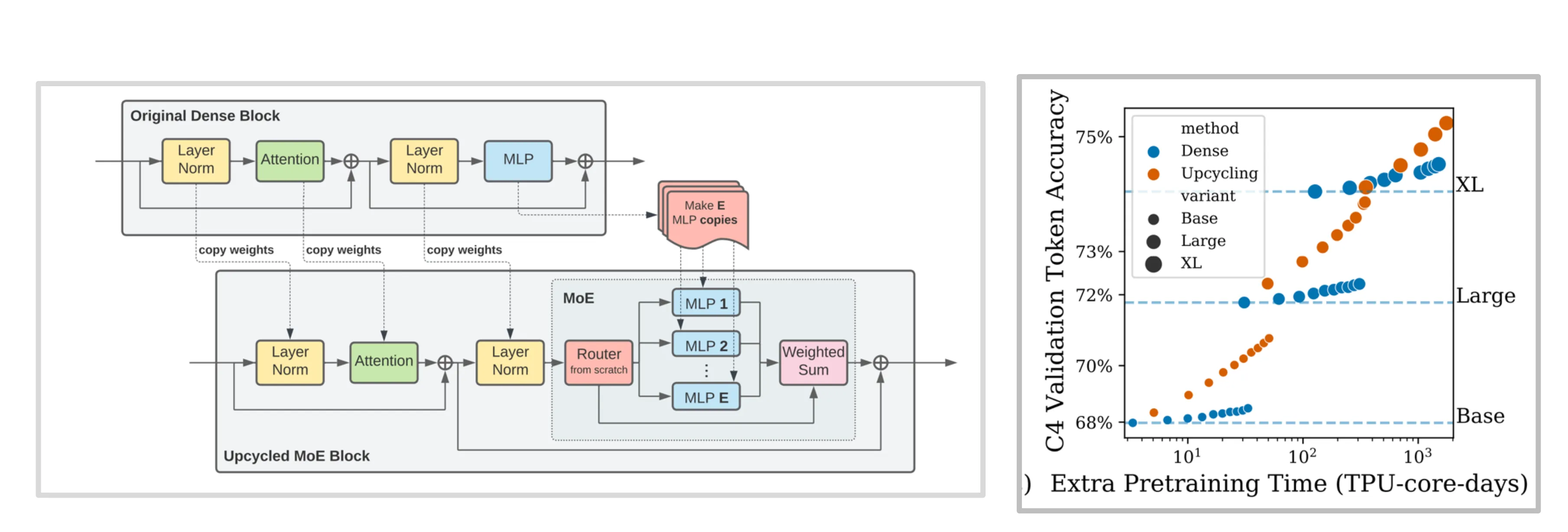
image.png

DeepSeek 演进路线

DeepSeek MoE V1

DeekSeek V1 是一个 16B 激活 2.8B 的模型，在架构方面选择了 2 共享专家 +64 细粒度专家，路由算法为 Top-6。使用了标准的辅助负载均衡损失函数。
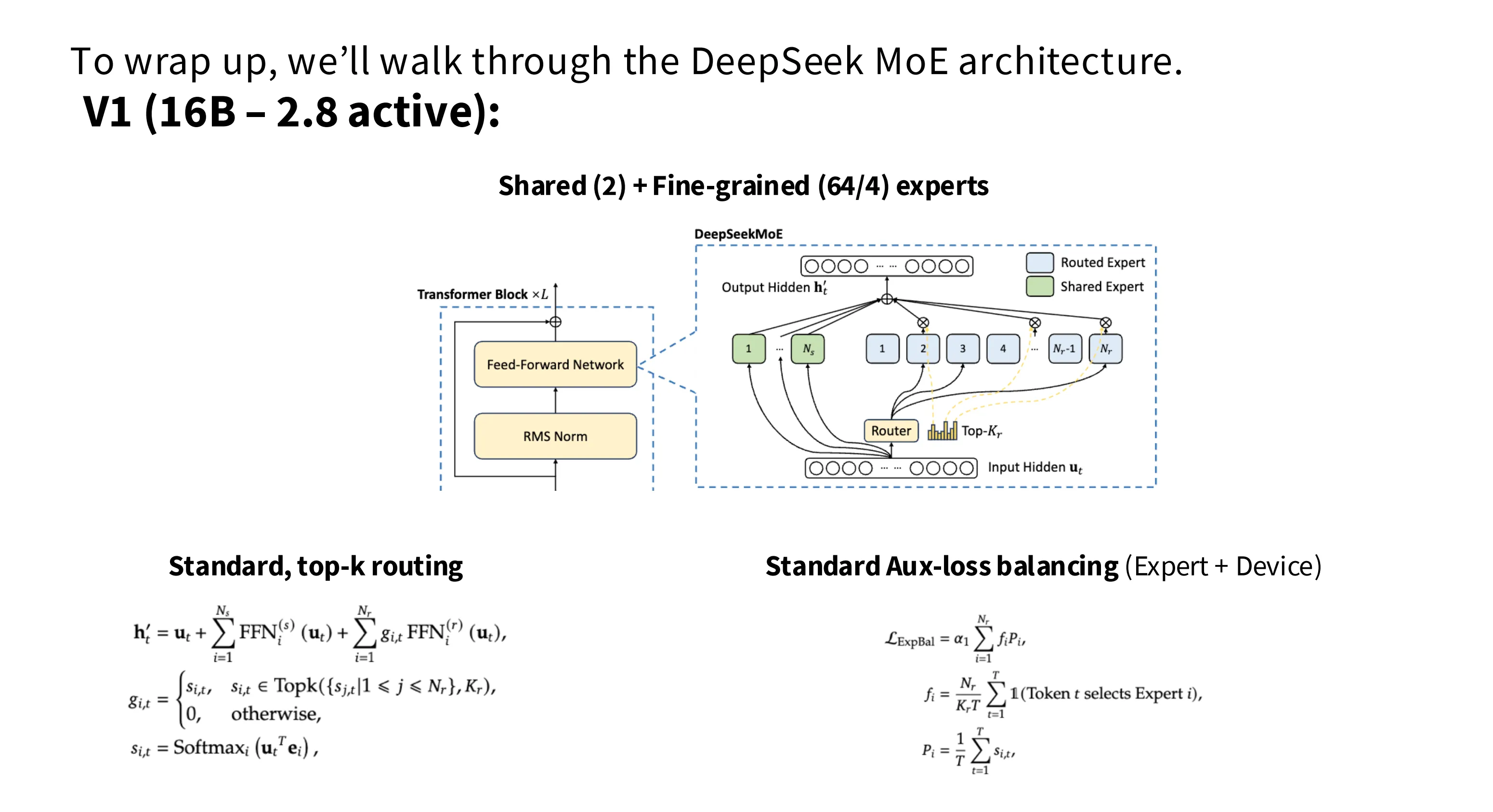
image.png

DeepSeek V2

V2 是一个 236B 激活 21B 的模型，采用 2 共享专家，160 细粒度专家，路由算法为 Top-6 。专家切分的越细，激活的专家就越多，因此引发的通信成本就越大。为此，在路由算法方面他们采取了两步走的策略，先选取 Tok-M 个设备，然后在这些设备上再进行路由，从而控制整体的通信成本。

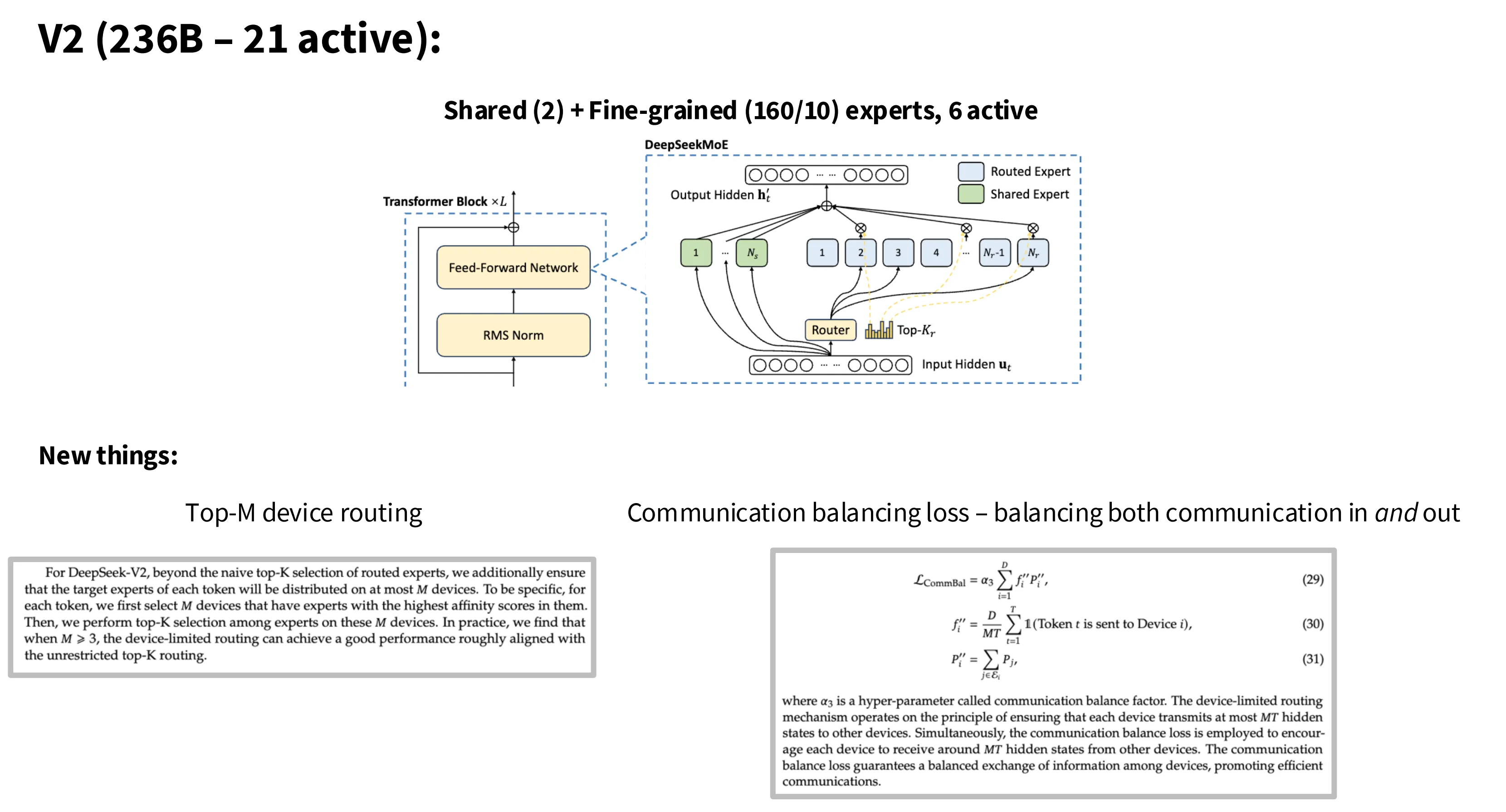
image.png

DeepSeek V3

V3 是一个 631 B 激活 37B 的模型，1 共享专家，258 细粒度专家，路由算法是 Top-8。在路由选择中，计算分数的函数从 Softmax 替换为 Sigmoid。在损失函数方面，其采用了之前提到的“无需辅助损失的启发式负载均衡”，同时采用了一个 sequence 级别的负载均衡损失函数，以确保 token 在推理阶段能够均匀派发给不同的设备。

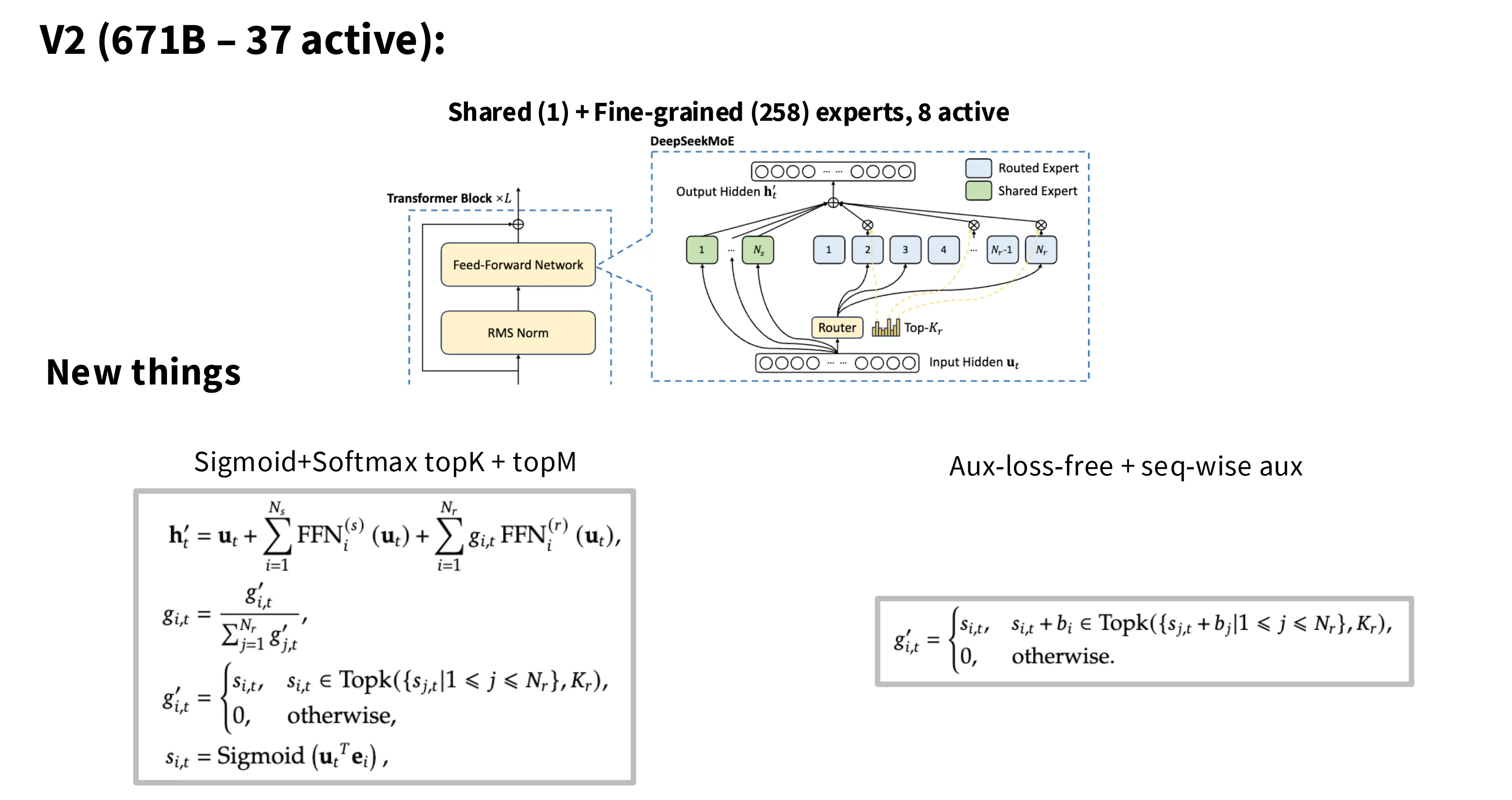
image.png

MLA & MTP

这部分老师讲的比较仓促，直接参考知乎上大佬的解读文章：
deepseek技术解读(1)-彻底理解MLA（Multi-Head Latent Attention）
deepseek技术解读(2)-MTP（Multi-Token Prediction）的前世今生