TL;DR 本讲梳理了现代 LLM 架构设计的“事实标准”（Post-Norm + RMSNorm + RoPE），并从系统视角解析了 GQA 与滑动窗口机制如何通过优化 KV Cache 访存，解决推理阶段的算术强度劣化问题。

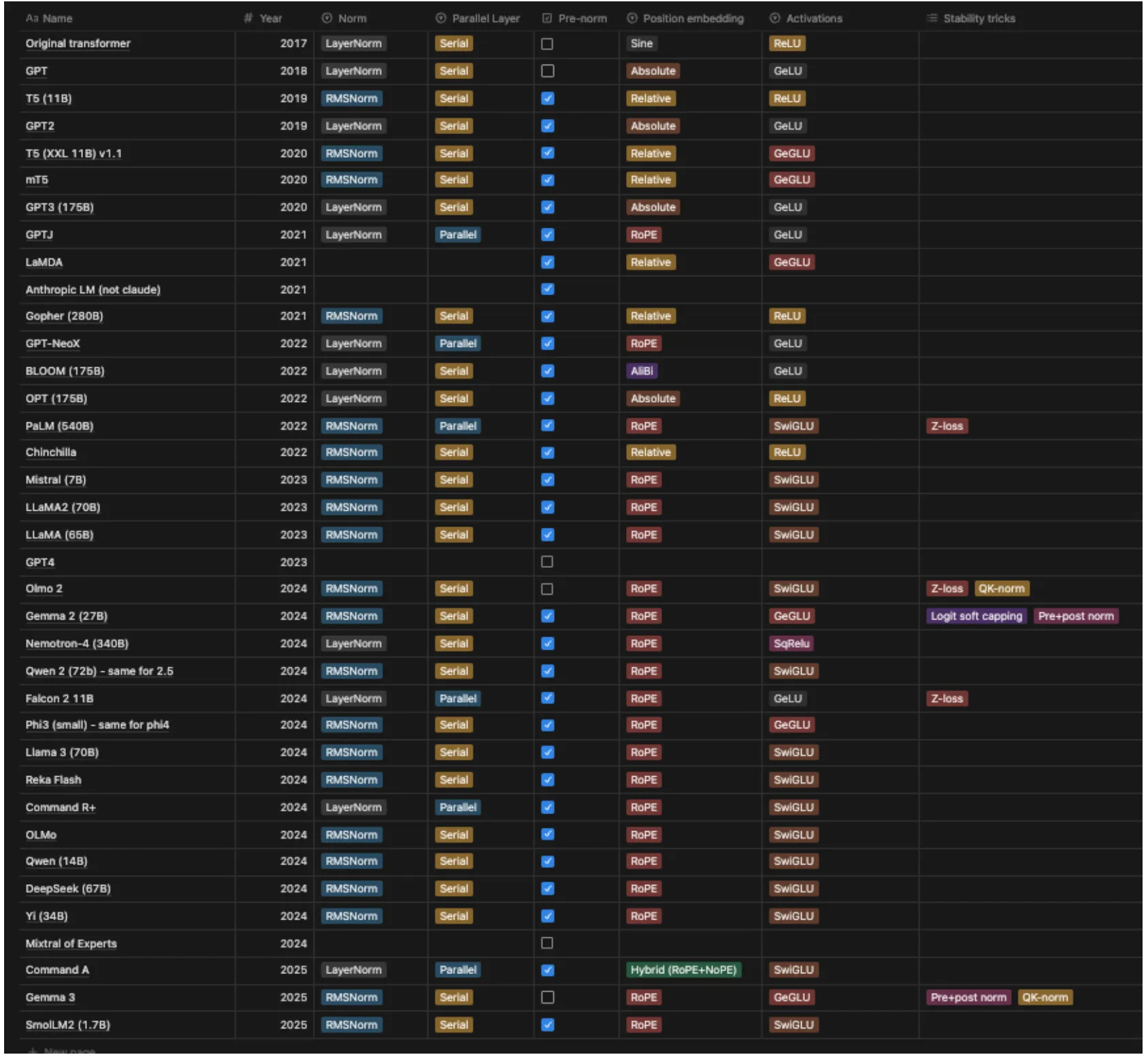
如下图所示，LLM Dense 模型的架构演进始于 2017 年。经历早期的百家争鸣与多方探索后，目前已呈现出明显的收敛态势。本讲将总结当前大模型在架构设计与超参数选择上的经验与技巧，旨在帮助我们立足前人成果，少走弯路。

具体来说，本讲包括：

  • 模型架构的变种
    • 激活层和全连接层的选择
    • Attention 的变种
    • 位置编码
  • 超参数的选择
    • ff_dim
    • 多头的 head_dim 之和是否一定要与模型的特征维度相等
    • 词汇表大小
  • 提升训练稳定性的技巧
  • Attention 架构
    LLM 模型架构演进路线

模型架构

Pre-vs-Post Norm

在标准 Transformer 架构中（下图左），Norm 块被安排在每个残差加法结束后进行，即 $x_{t+1}=\text{LayerNorm}(x_t+F(x_t))$，这是 Pre-Norm。而在 Post-Norm 中（下图右），Norm 被放在残差内的子层之前，即 $x_{t+1}=x_t+F(\text{LayerNorm}(x_t))$。
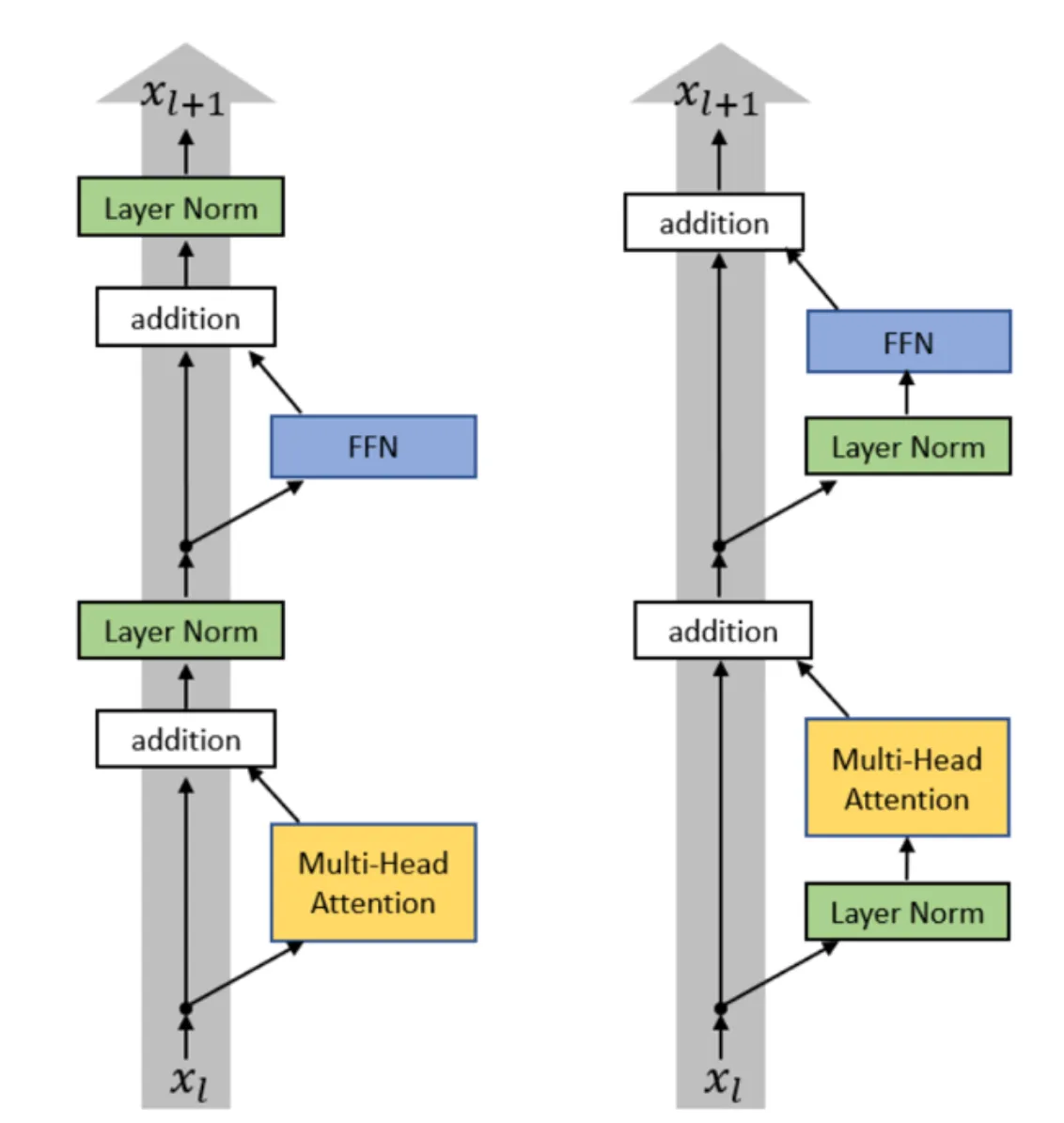
Pre-vs-Post norm

从 2024 年起，使用 Post Norm 替代 Pre Norm 成为业界广泛共识， Post Norm 在训练稳定性上优于 Pre Norm。 在 Pre-Norm 中，需要引入一些提升稳定性的 tricks ，例如 Warm Up ，来确保训练稳定进行；而在 Post Norm 对此则没有那么敏感，并且最终的模型性能与 Pre-Norm 不相上下。

为啥 Post Norm 更好？主流的解释是在 Post Norm 的残差路径上不存在 Norm 模块，梯度可以通过恒等映射直接从顶层传播到底层，从而避免了梯度消失或者爆炸问题。当下的模型越来越深，训练的稳定性就是刀乐，业界普遍转向 Post Norm 也是个很符合直觉的现象。

既然 Pre Norm 是在残差的子层计算前进行 Norm，是不是有工作尝试在残差子层计算后进行 Norm 呢？有的，包有的。老师将其成为 Double Norm，即在残差子层计算前后都进行一次 Norm，近期的 Gemma 2 就采用这种架构。
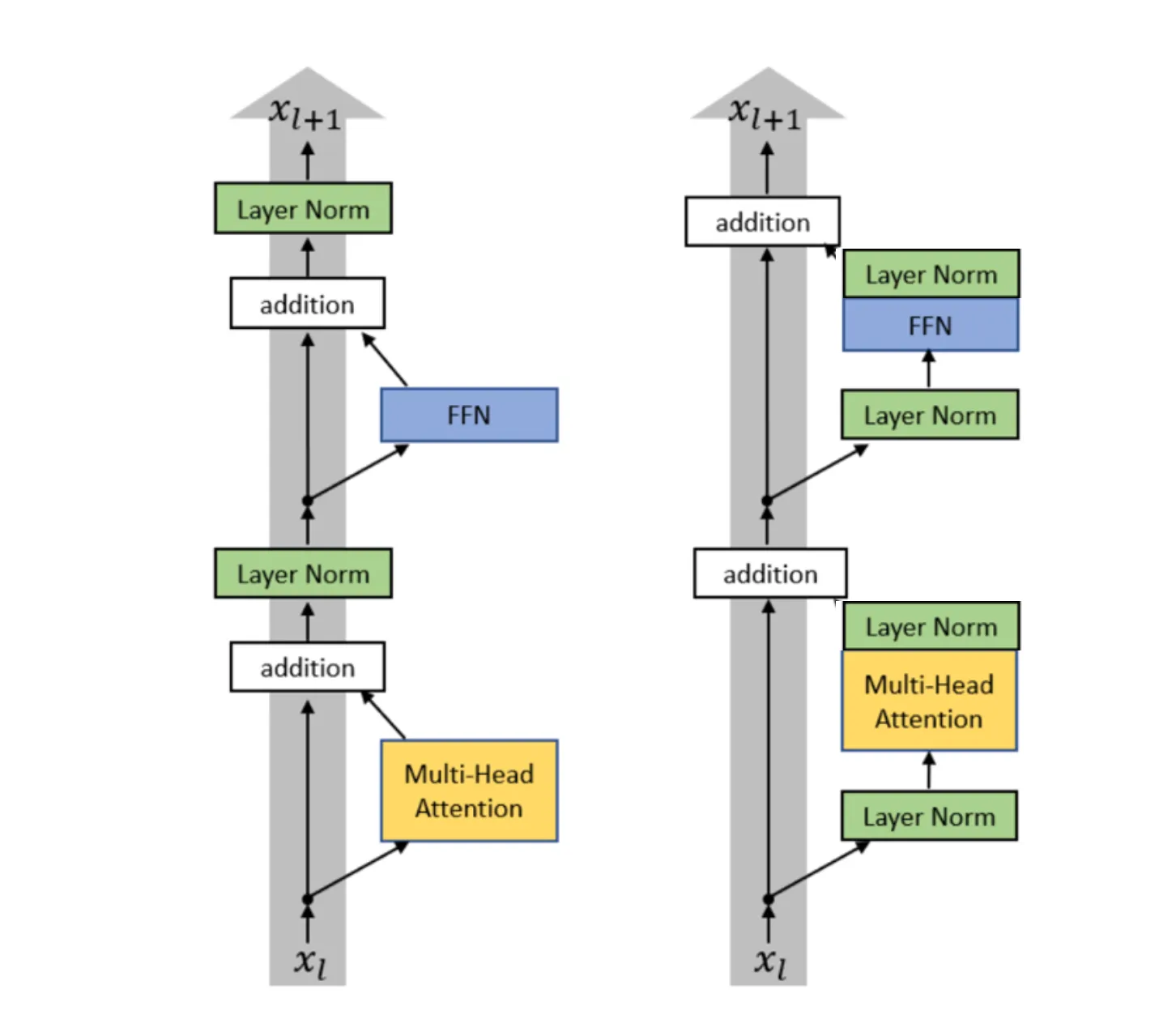
Double Norm

LayerNorm vs RMSNorm

LayerNorm 与 RMSNorm 公式如下，前者在特征维度进行标准化后按照两个可学习的向量 $\gamma$ 和 $\beta$ 缩放和偏移，后者省去了对均值偏移的操作，

$$ \begin{align*} \text{LayerNorm(x)} &= \frac{x - \mu}{\sigma} \cdot \gamma + \beta \\ \text{RMSNorm}(x) &= \frac{x}{\sqrt{||x||^2_2+\epsilon}} \cdot \gamma \end{align*} $$

近年来，业界普遍从 LayerNorm 转向了 RMSNorm。 这一转变可以归结为：RMSNorm 计算量和参数量都更少。如下图所示，就理论计算量而言，Norm 模块占比只有 0.17% 并不高，但是由于需要搬运显存，导致了在实际运行中占比高达 25.5%，省略对均值的偏移可以降低对显存读写的需求，从而提升实际运行速度。与此同时，模型的精度并没有因为这一转换而降低。

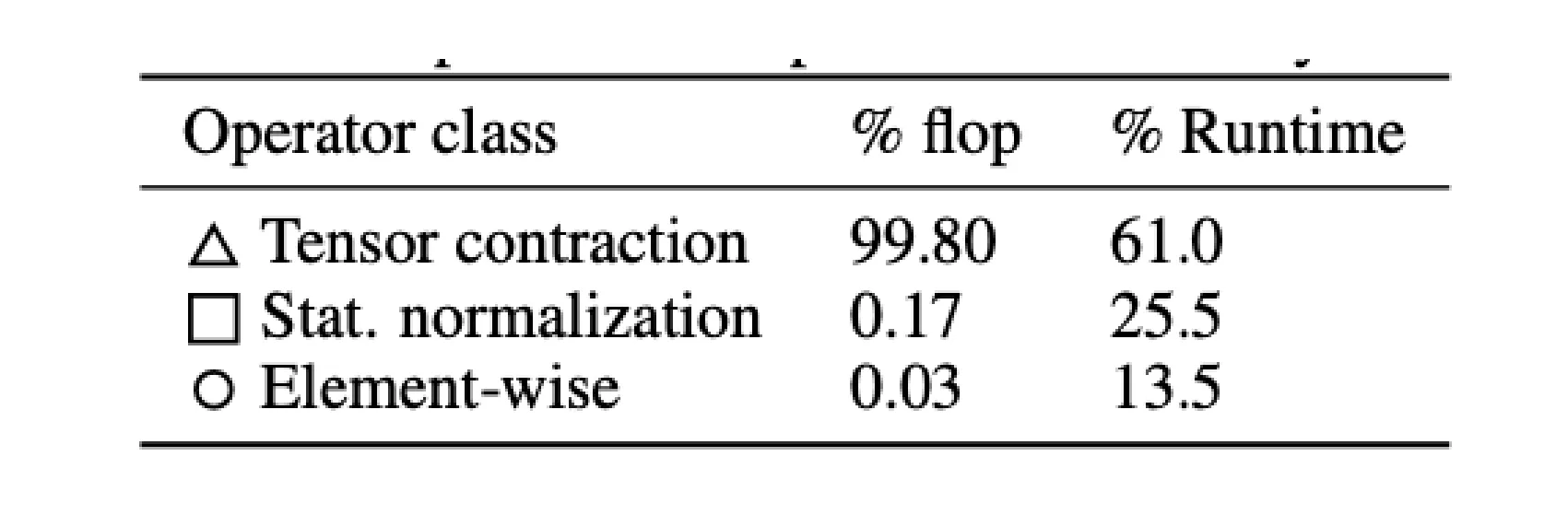
LLM 各模块计算量和运行时占比

在 Norm 模块，另一潮流是现代模型倾向于扔掉偏置项。 不只是 RMSNorm 的偏置项，还包括所有线性层中的偏置项。这一转变的底层动机与 RMSNorm 一致：减少内存开销。此外，尽管还说不清楚，但是确实有现象表明丢弃偏置项可以提升学习过程的稳定性。

激活函数

激活函数有很多很多，采用不同的激活函数，可以衍生出各种 MLP 的变种。这里直接用课程里的 PPT 来介绍：

ReLU 是最简单的激活函数，但是在负值区域没梯度，可能导致神经元饿死。GeLU 在负值区有微小梯度仍可以继续训练。
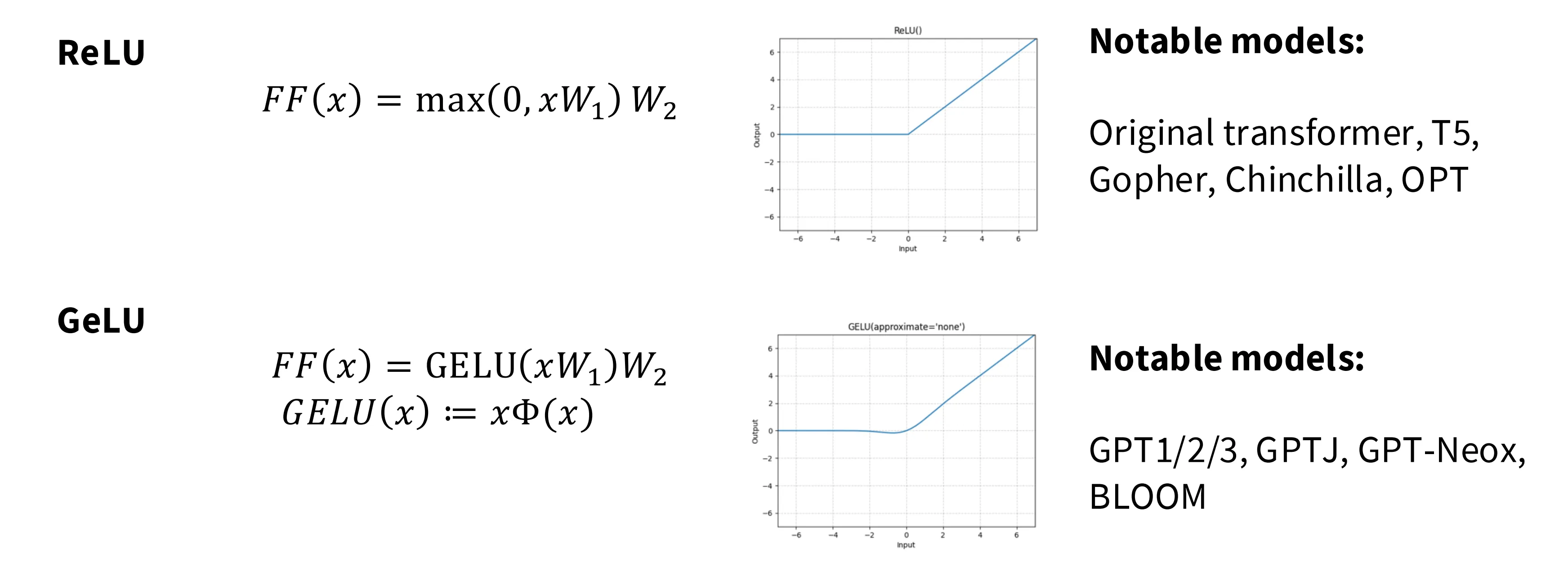
image.png
*GLU 系列的 MLP 层修改了第一个全连接层，将其额外逐元素乘上一个 $xV$，实现所谓“门控机制”。
image.png
根据激活函数的不同，产生了 ReGLU、GeGLU 和 SwiGLU 的变种，其中门控单元中特征维度长度为模型特征维度的 2/3 以确保整体参数量和计算量不变。
image.png
实验表明 GLU 系列确实具有更好的表现，但是也不是必须的，例如 GPT-3 就没有使用这一激活函数。

并行与串行架构

传统的 Transformer 架构属于串行架构，输入依次经过 LayerNorm、 Attention 、残差、MLP 和 MLP 模块；与之相对的变种是并行架构，输入同时经过 Attention 和 LayerNorm 模块，然后将两个模块的输出相加并送入 MLP。这一设计使得模型在大规模训练时能够提升一定的训练速度。

位置编码

在 LM 早期，有各种位置编码函数，包括 Sine、绝对位置编码、相对位置编码：
image.png
有了以上这些函数，为啥还需要 RoPE 呢？一个完美的相对位置编码应该满足如下的数学定义：对于一个位置嵌入函数 $f(x, i)$，我们希望两个被位置嵌入后的向量的点积（也就是注意力分数）只和这两个向量的相对位置有关，也就是：

$$ \text{InnerProduct(f(x, i), f(y, j)) = g(x, y, i-j)} $$

上述性质也可以被描述为平移不变性。

为了实现平移不变性，RoPE 的思路是将一个每个 token 都根据其位置旋转对应角度，这样在计算二者的夹角时就仅与二者相对位置相关。每个 token 在特征维度构成的空间是高维的，而角度是一个在二维平面上的概念，为此 RoPE 的解决方案是将特征维度两两分组，每组视为一个二维向量进行旋转操作，并且不同组的旋转角度不同，从而同时捕获高频和低频位置信息。

小节

  • Pre-vs-Post Norm
    • 选 PreNorm，更稳定
  • LayerNorm vs RMSNorm
    • 果断选 RMSNorm，更快，模型性能有时更好
  • 激活函数
    • GLU 系列似乎更好，但是差距并不显著
  • 并行与串行架构
    • 没有严格的消融实验证明并行更好
    • 并行在计算速度上有一定的优势
  • 位置编码
    • 果断选 RoPE，其具备平移不变性

超参数

MLP 特征数

在 MLP 模块中，会将输入的特征的维度从模型维度 $d_{\text{model}}$ 在内部投射到 MLP 特征数 $d_{\text{ff}}$。对于非 GLU 系列的 MLP 模块，一般将其放大 4 倍；对于 GLU 系列的模块，一般将其放大 8/3 倍。这是目前的共识。

有工作研究过上采样倍数与 loss 的关系，结果显示倍数在个位数这个数量级上效果最好。曾经有工作（T5）选择了 64 的倍数，但是那也是昙花一现，在其后续的 T5 v1.1 中也选择了常见的 2.5 倍作为上采样系数。
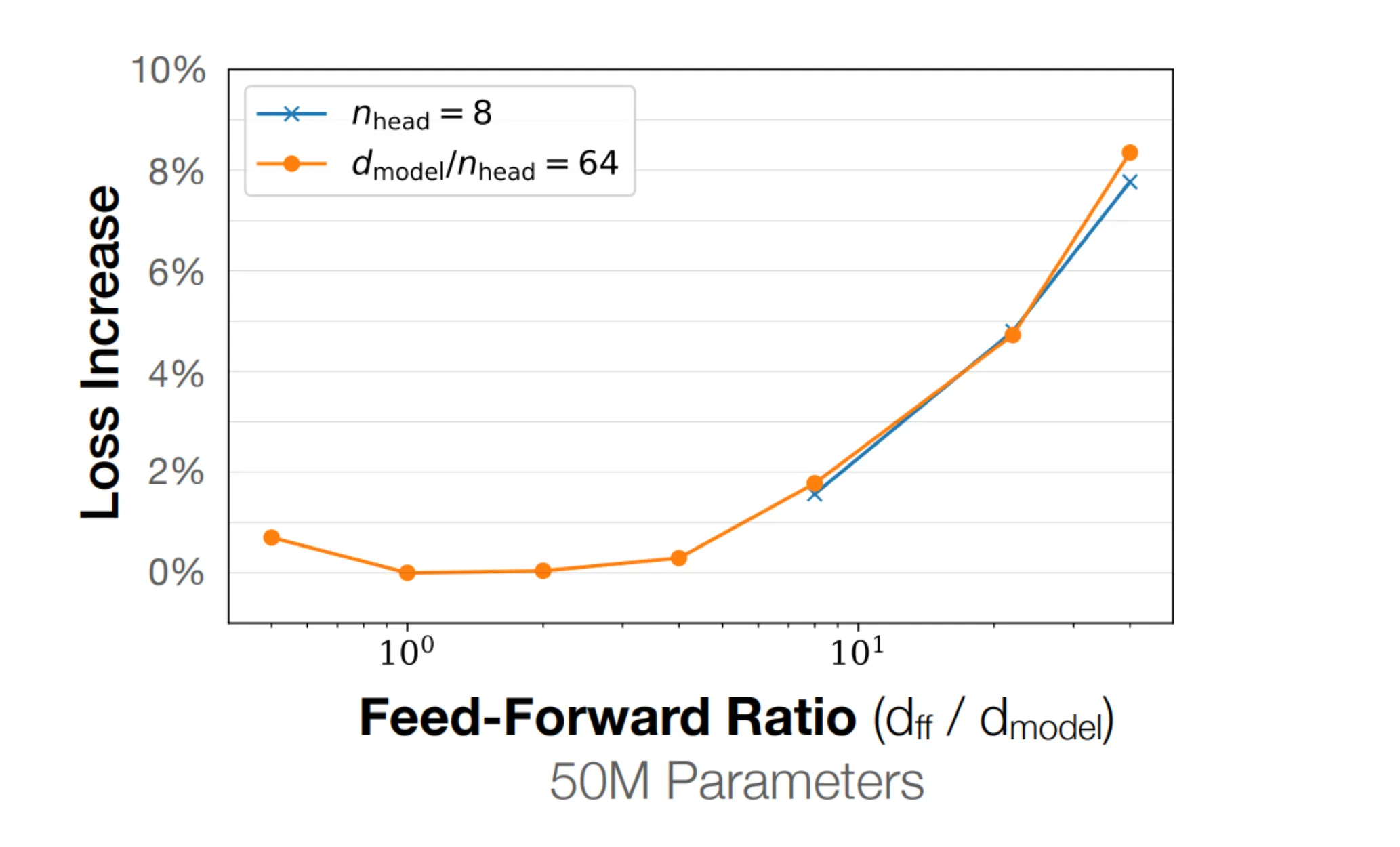
image.png

注意力特征数

本节讲的是 num_heads x head_dim 这一组超参数的选择，我将其描述为注意力超参数。

目前业界的共识是注意力特征数等于或者略多于模型特征数。

对于这个参数的选择，有工作认为当固定总特征数后，如果想要提升头数，就不得不降低每个头的特征数，这会导致每个头的表征能力下降，进而降低模型的整体性能。但是在实践中这一效应并不显著，业界还是倾向于使用模型特征数作为注意力的特征数。
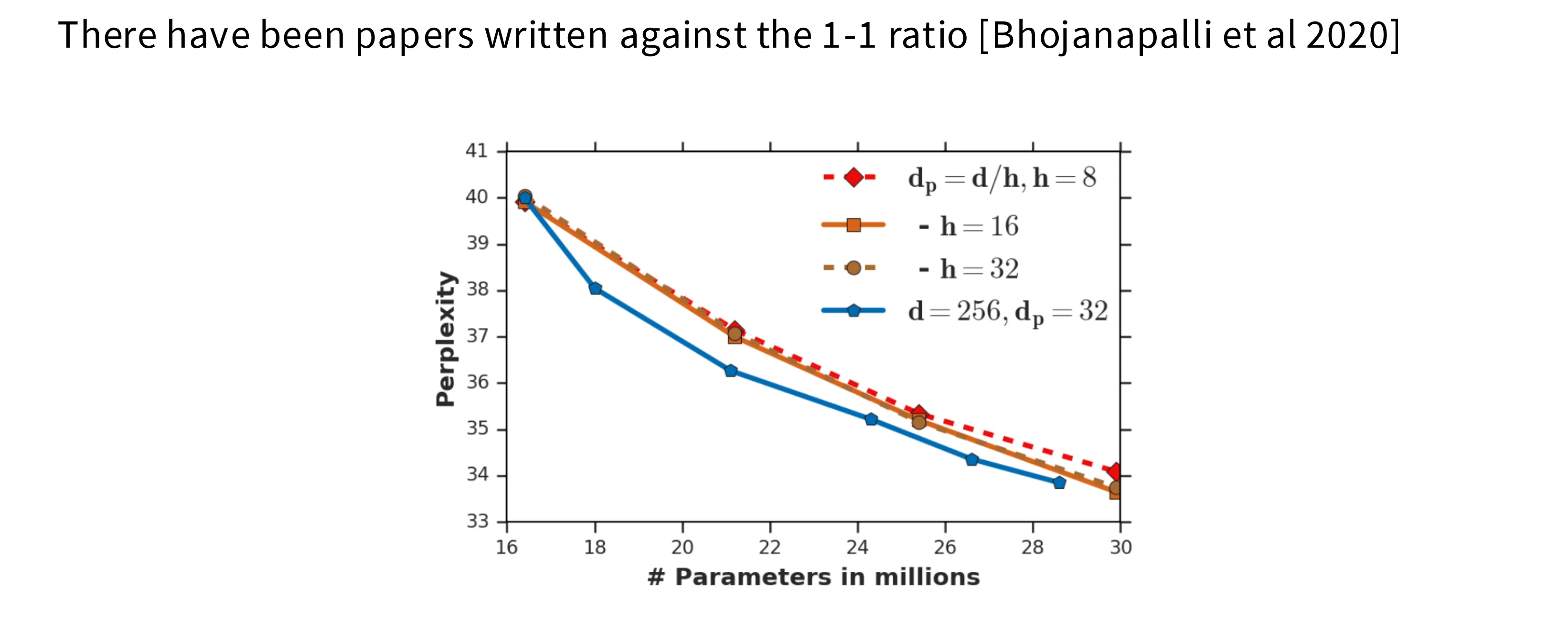
image.png

横纵比

横纵比指的是模型的特征数与模型的深度 num_layers 之间的比值。主流模型选择 1xx 这个区间，这似乎也是一种共识。

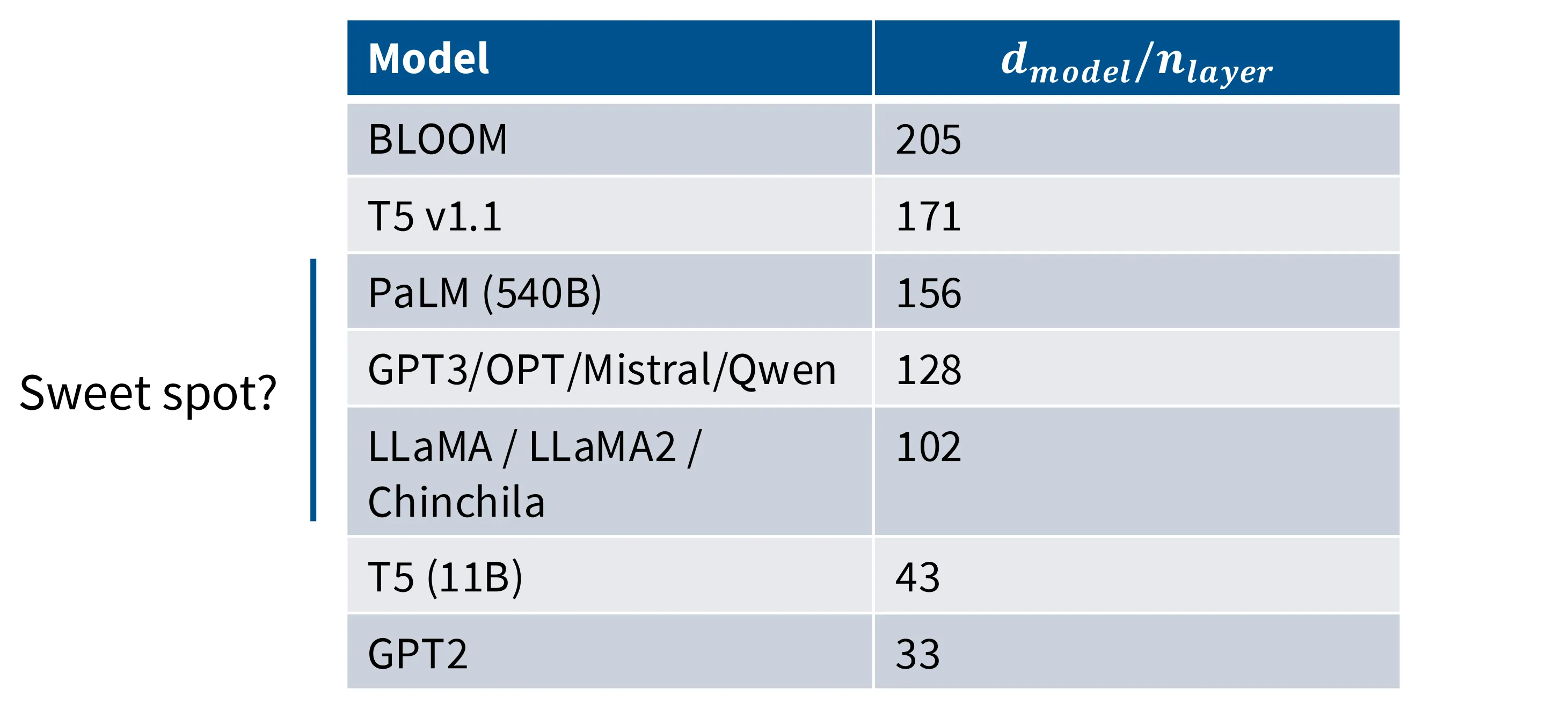
image.png

相关工作也证实了 1xx 这个区间是比较好的一个甜点区，与模型参数量相关性并不显著。
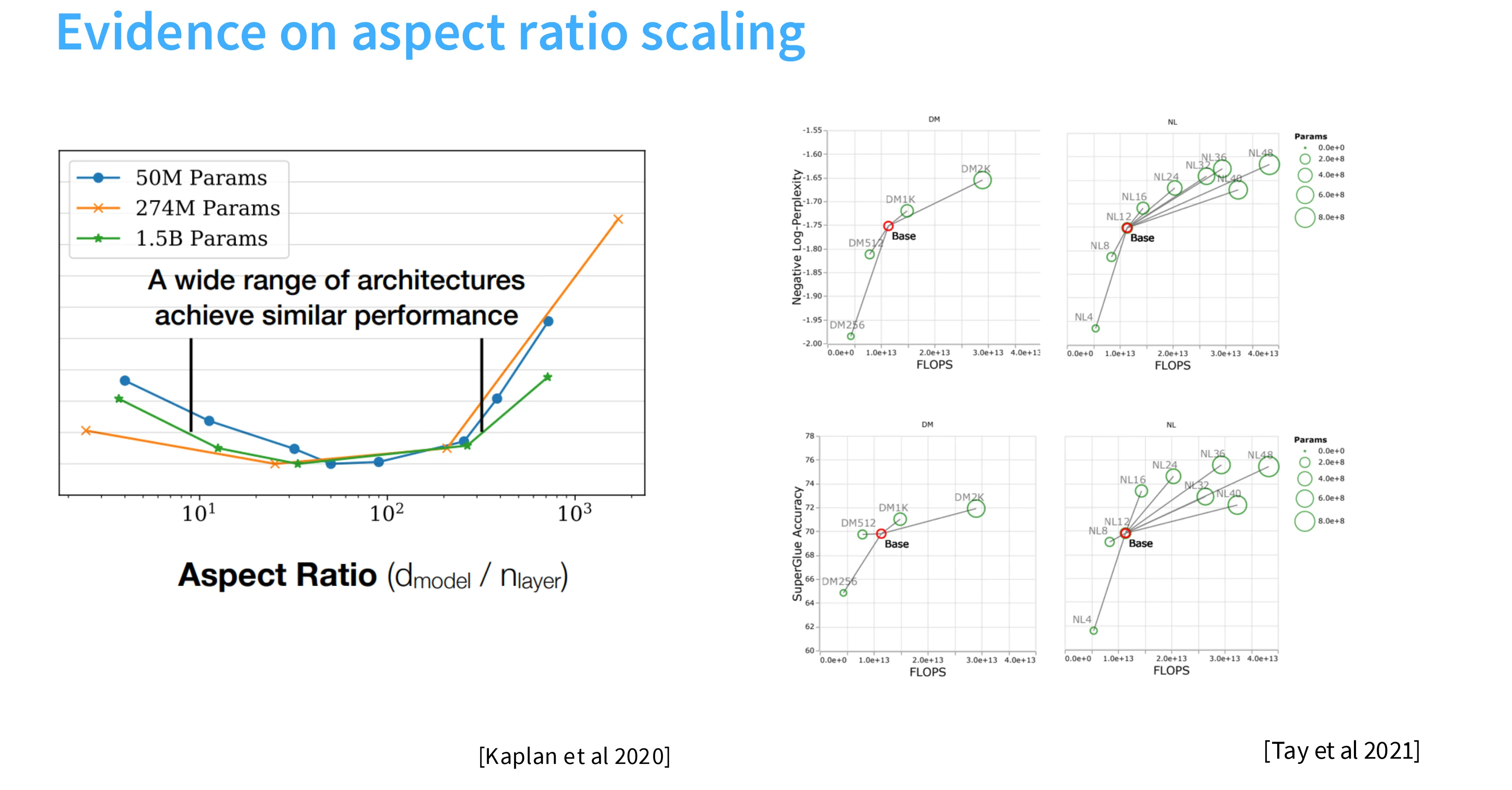
image.png

横纵比影响着并行策略的选取，比较深的模型适合流水线并行，比较胖的模型适合张量并行。

词汇表数量

词表的数量取决于支持的语言数量和具体生产用途，单语言模型在 30-50k 这个量级，多语言模型在 100-250k 这个量级：
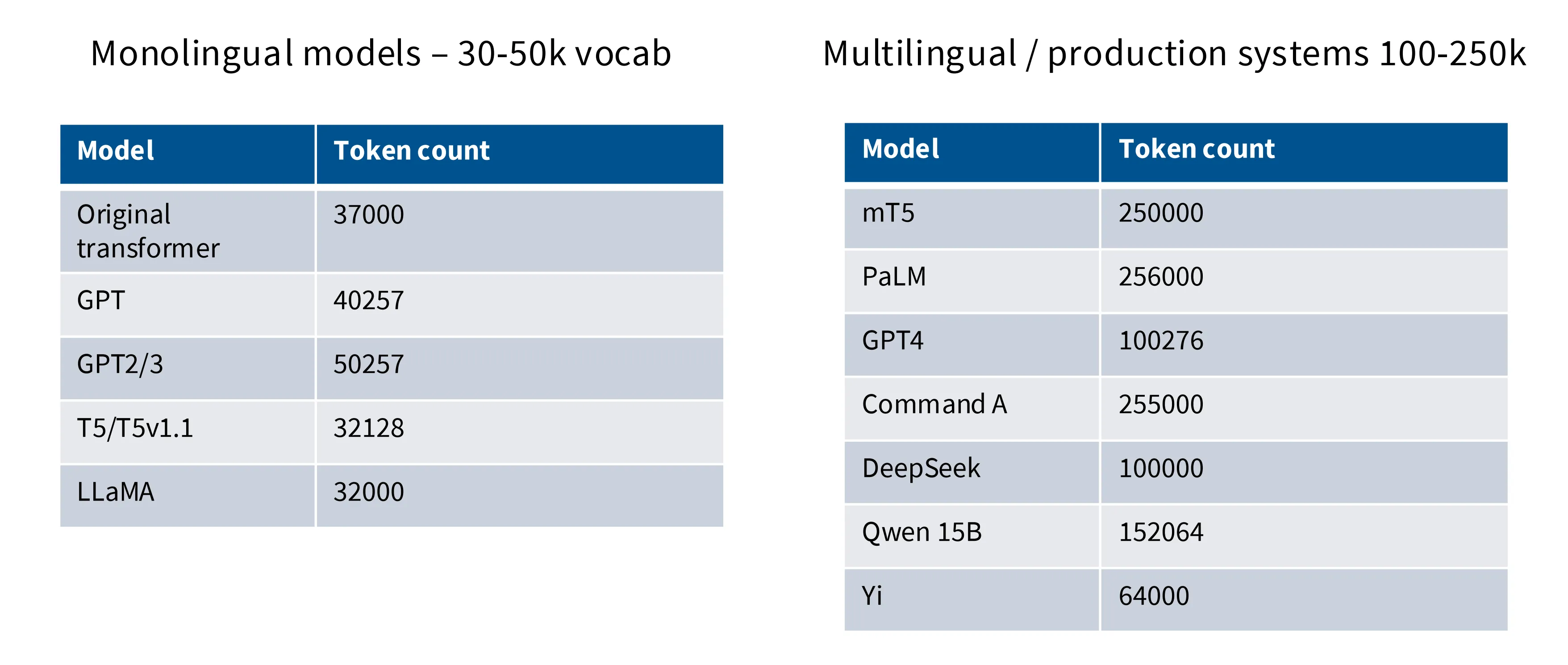
image.png

正则化

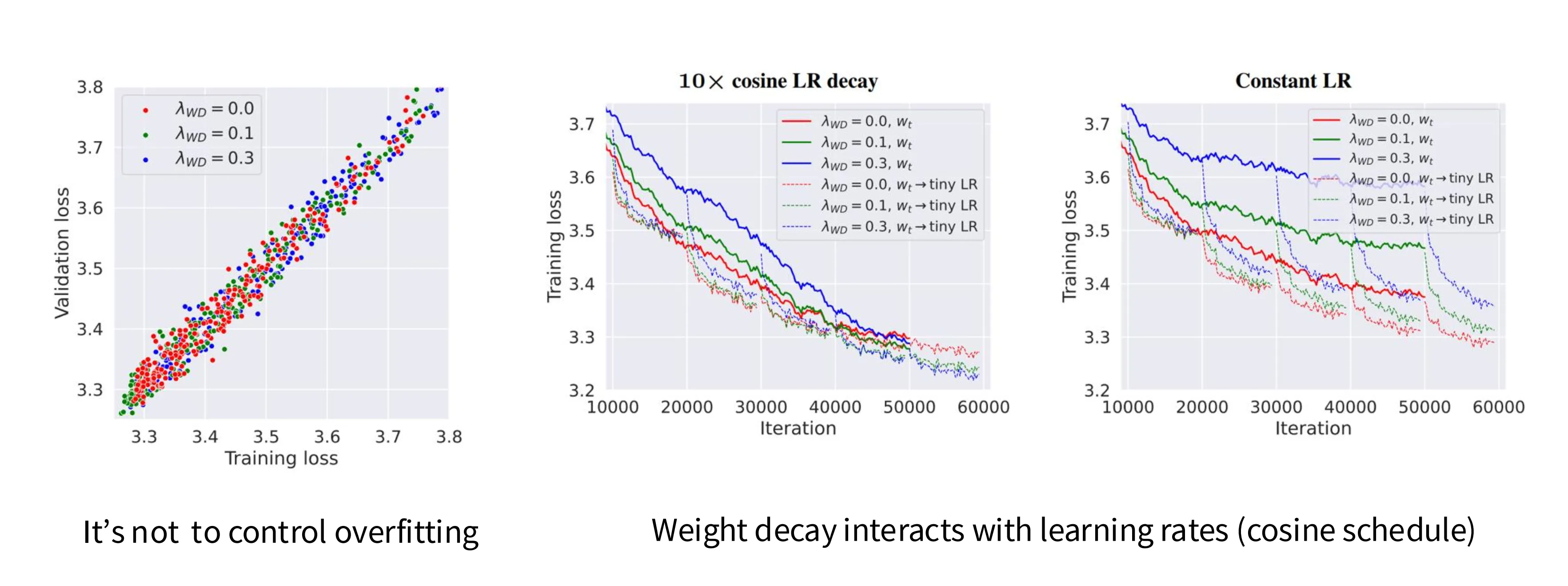
理论来说，在预训练阶段不需要正则化手段（Dropout、Weight Decay），因为预训练阶段在训练数据上跑一轮，很难产生过拟合。但事实上，大家倾向于使用一些正则化技术：
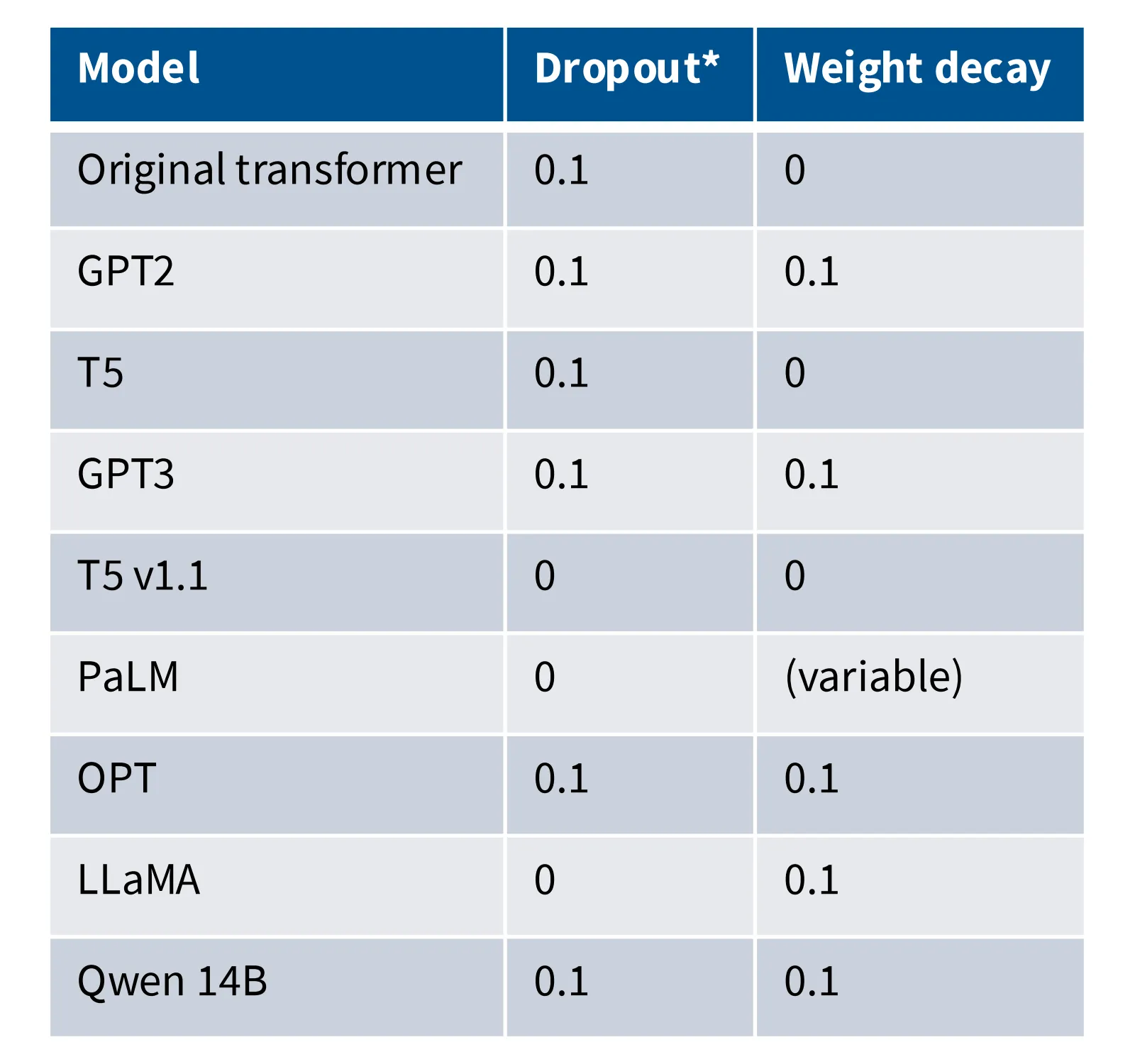
image.png

对于这一反直觉的现象，一篇工作对此的解释是：Weight Decay 不是为了防止过拟合，它是一种与学习率相互交互的技巧，将权重变小在某种程度上等价于将学习率变大，这可以让模型在训练后期学习率较小的时候获取一个更小的损失值。

image.png

小结

  • MLP
    • GLU 系列选择 8/3 作为上采样系数
    • 非 GLU 系列选择 4 作为上采样系数
  • 注意力特征数
    • 注意力特征数等于模型特征数
  • 纵横比
    • 选择 1xx 作为纵横比
  • 正则化
    • 使用正则化手段，但是是为了获得更小的损失

技巧

本节将介绍一些训练过程中提升稳定性的技巧。

Softmax

Softmax 计算中由于存在 exp 和除法操作，因此其对数值很敏感，例如除 0 等问题，很容易在训练过程中爆炸。在 Transformer 中有两处 Softmax，一处是模型最后对 logits 进行 Softmax 操作，另一处是 Attention 块中计算注意力得分时的 Softmax 操作。下面针对这两处分别介绍提升稳定性的技巧。

  • Output Softmax
    记 Softmax 中的分母项为 Z，为了防止 logits 中 Z 过大，引入了一种叫做 Z-loss 的优化手段，即将 log(Z) 作为正则项加入到损失函数中，迫使 Z 优化到 1 附近，从而避免在大规模计算中的指数运算引发浮点数溢出和梯度异常。

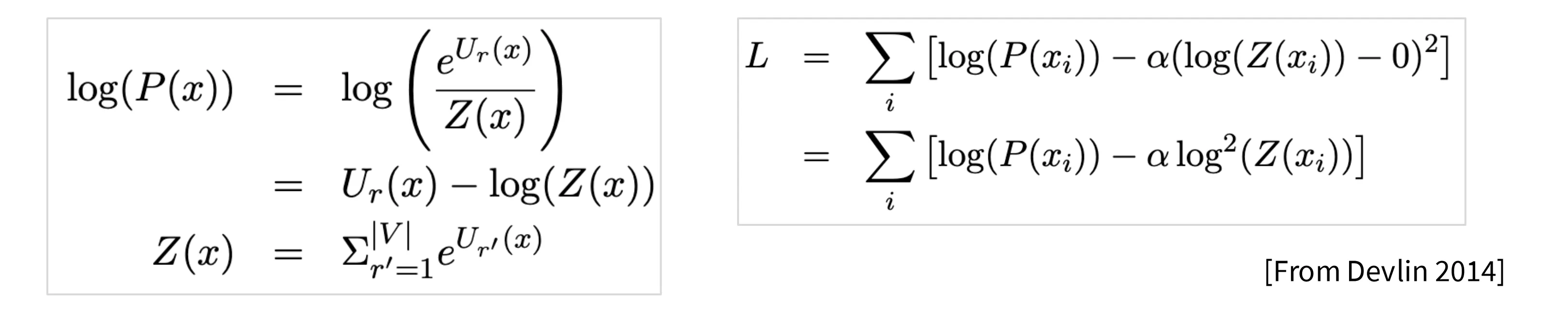
image.png

  • Attention Score
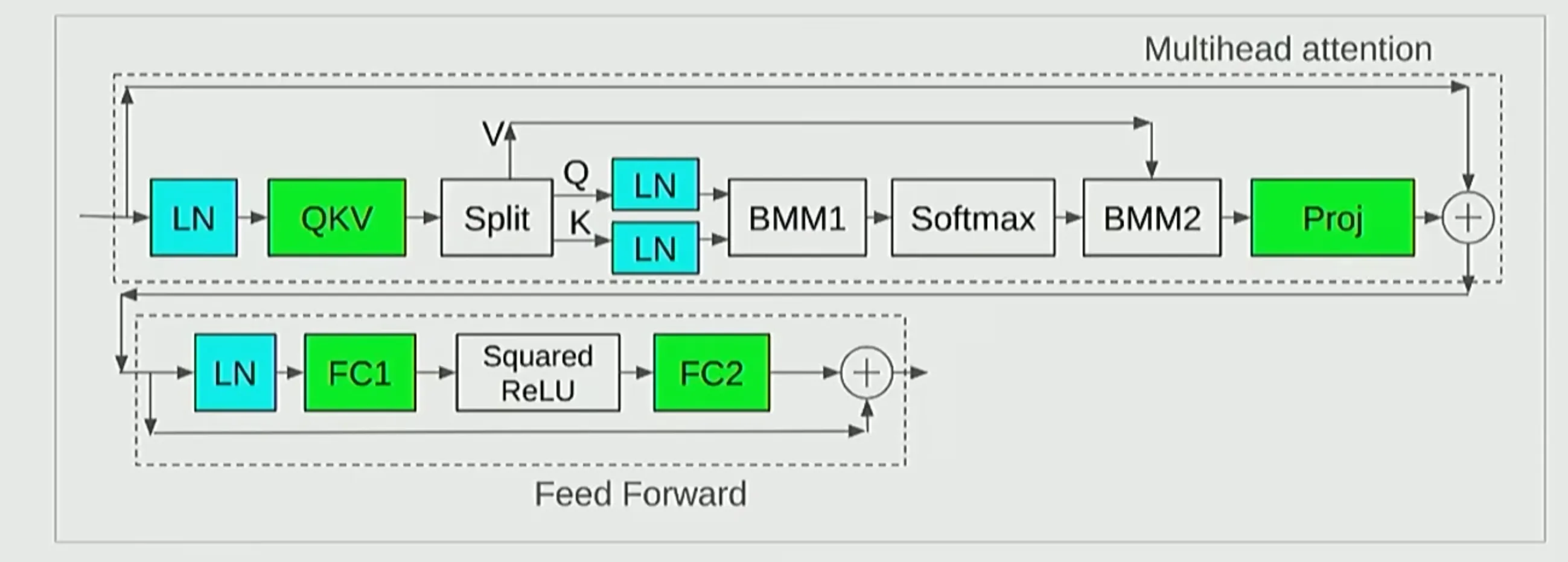
    在 MHA 计算中，一些视觉和多模态模型在 QK 计算注意力分数前分别对 QK 计算一次 LayerNorm，这一技术被称为 QK Norm，能够提升训练过程中的稳定性。
    image.png

Attention 机制

GQA / MQA

如下图所示，在 LM 的训练阶段，Attention 模型具备比较高的算术强度 Arithmetic Intensity（下图中 k 应该是 d），即在训练阶段是计算受限的，这能够充分发挥 GPU 的计算能力。
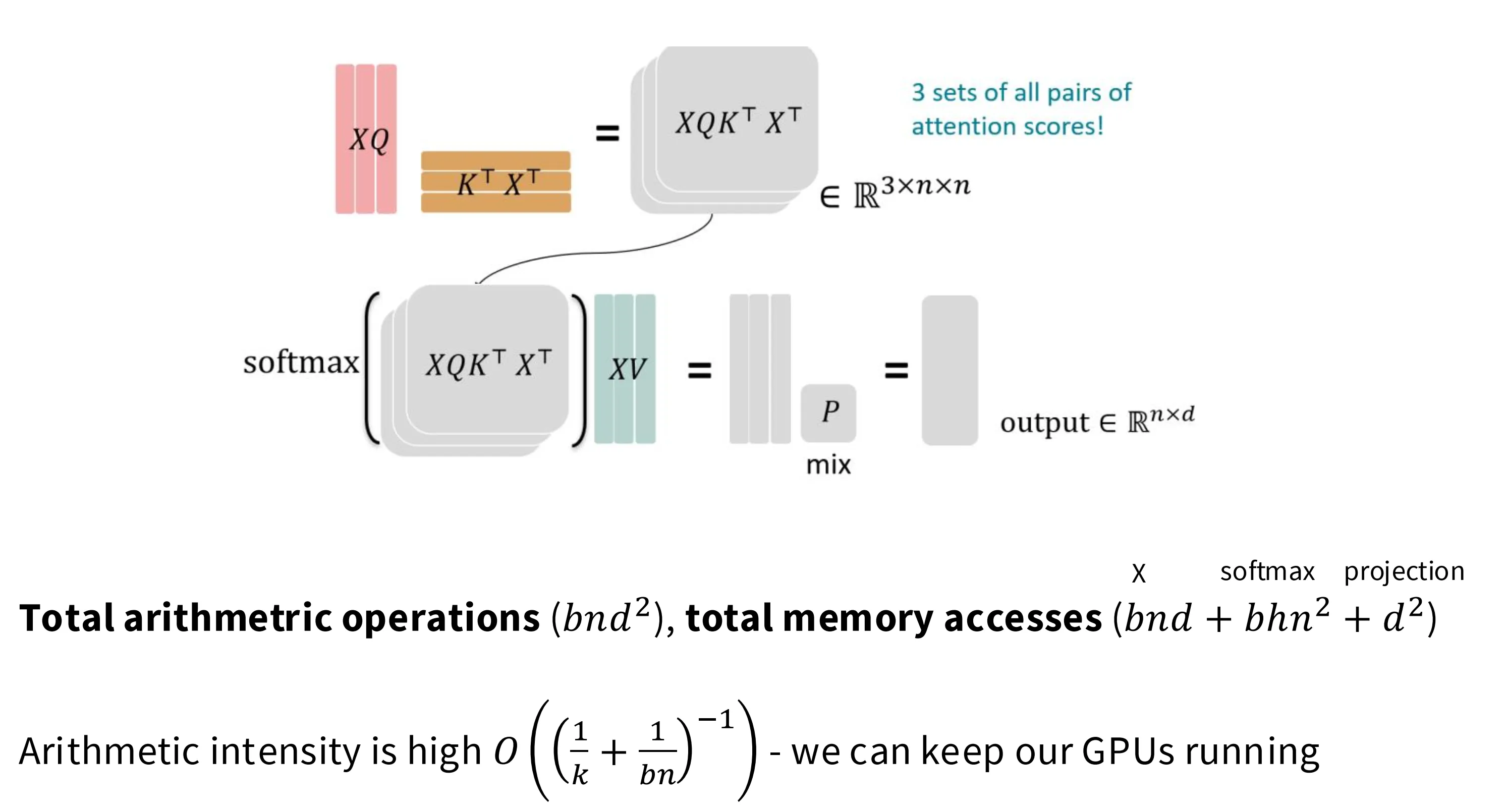
image.png

但是在推理阶段，我们无法并行地去预测每一个 token，只能逐 token 生成。如下图所示，当生成 t+1 个 token 时，前 t 个 KV 值可以被 Cache，在 qkv 的 projection 阶段，只需要计算 input 中最后一个 token 的对应的 qkv。
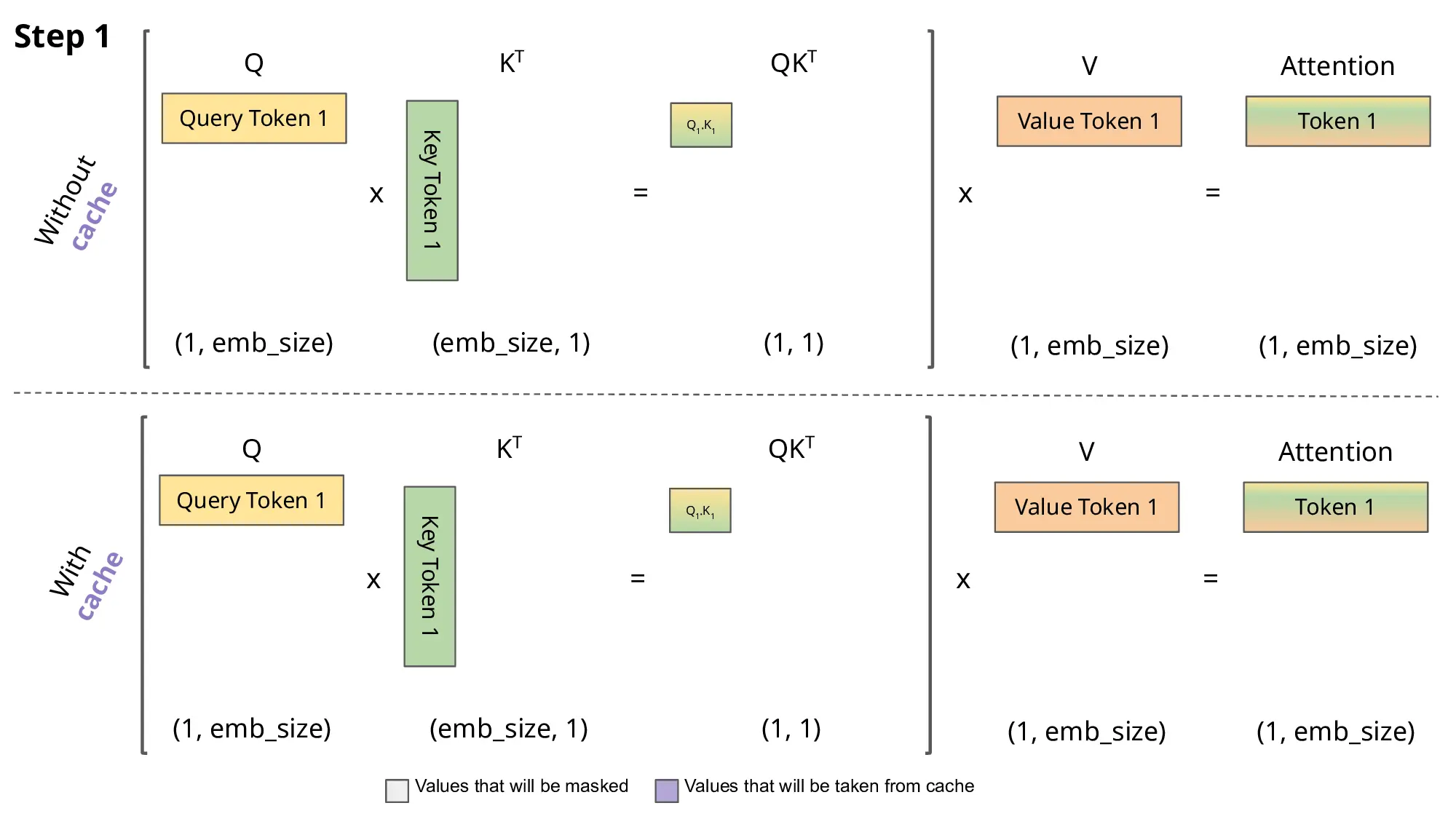
KV Cache 示意图 图源：https://medium.com/@joaolages/kv-caching-explained-276520203249

带有 Cache 的 MHA 中，总的计算量并没有变（训练一次性计算出所有的 QKV，推理分 n 步计算出所有的 QKV），但是总的访存量显著增加，因为需要反复加载 Cache，最终导致算术强度在推理阶段劣化。
image.png

导致算术强度劣化的原因是 KV Cache 的反复加载，解决问题的思路是减少 KV Cache 的大小。KV Cache 来自 KV Projection，因此一个很自然的想法是减少 KV 的注意力头数。如果将头数减少到 1，就是 MQA（Multi-Query Attention），此时的计算强度随着注意力头数的增加而增加。如果将 KV 的头数降低为 Q 的 1/n，即每一个 KV 对应 n 个 Q，这就是 GQA（Group Query Attention），同样可以提升算术强度。
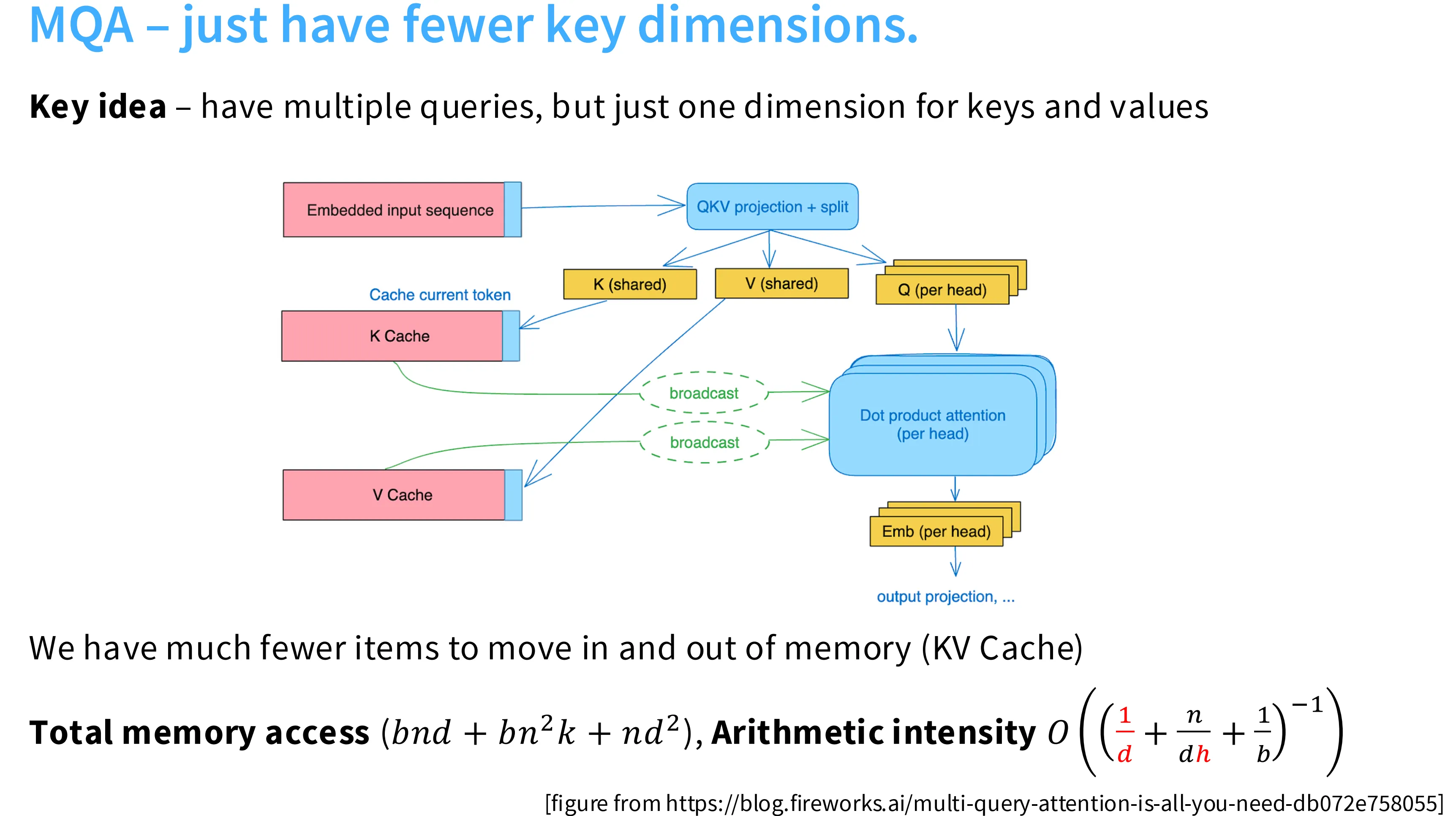
MQA 示意图

Sparse/Sliding Window Attention

在传统 Attention 中，每个 token 会与其之前所有的 token 交互生成注意力分数，这使得 Attention 计算量和 KV Cache 的长度随 N 增长而平方和线性增长。

如下图所示，在滑动窗口注意力中，每个 Token 只与其附近固定数量个 Token 交互，从而使得总计算量随 N 线性增长。
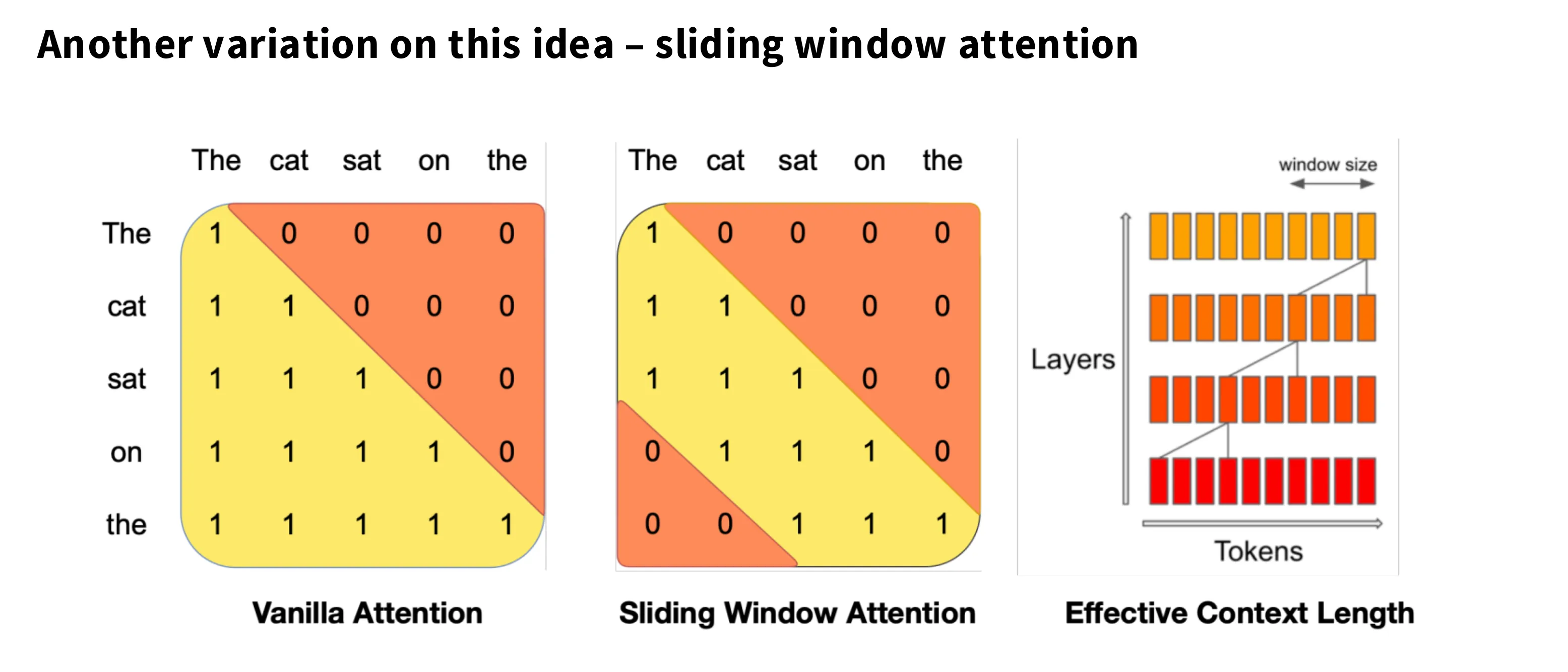
image.png

对于稀疏注意力，老师没有太多的介绍，Gemini 对此的概括是：为了解决 Sliding Window “目光短浅”的问题，Sparse Attention 引入了更复杂的连接模式，包括：滑动窗口，保留 Sliding Window，用于捕捉局部语法关系；全局节点，定几个特殊的 Token（比如 [CLS] 或者特定的 prompt token），让它们可以看到所有人，所有人也可以看到它们；空洞，像空洞卷积一样，每隔 $k$ 个词看一眼。增加了感受野，但不需要全看。

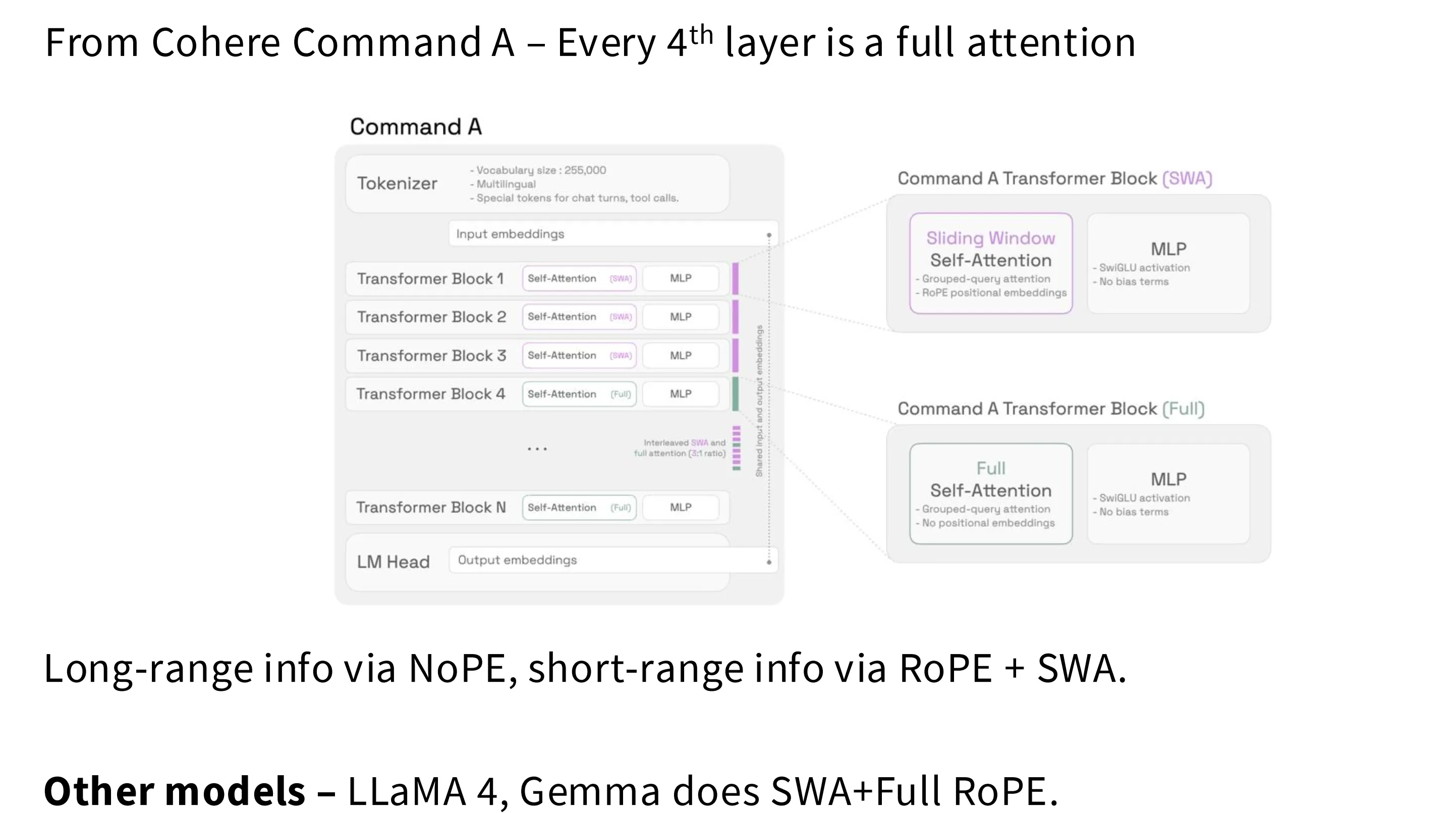
Trick

为了同时获取稠密 Attention 全局感受野和稀疏 Attention 减少计算量的收益，现在有一种架构同时使用上述两种 Attention。以 4 个 block 为一个周期，前三个使用稀疏注意力，第四个使用标准注意力。在某些实现中，仅在滑动窗口注意力中使用位置嵌入 RoPE，在全量注意力中不做位置嵌入

image.png